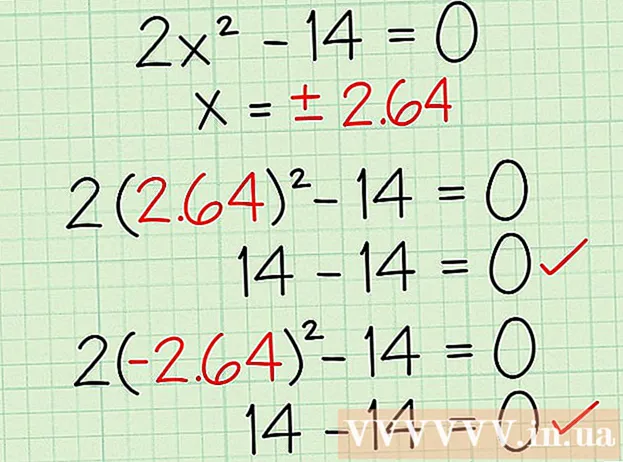
Indhold

• Trin
• Råd
• Advarsel

To fraktioner kaldes ækvivalente, hvis de har den samme værdi. At vide, hvordan man konverterer en brøk til dets ækvivalente former, er en væsentlig matematikfærdighed for alt fra grundlæggende algebra til avanceret matematik. Denne artikel introducerer flere måder at beregne ækvivalente fraktioner fra grundlæggende multiplikation og division til mere komplekse metoder til løsning af ligninger med ækvivalente fraktioner.

Trin

Metode 1 af 5: Opret ækvivalente brøker

1. 

   Multiplicer tælleren og nævneren med det samme nummer. Per definition har to forskellige, men ækvivalente fraktioner tælleren, og nævneren er multipla af hinanden. Med andre ord multiplicerer tælleren og nævneren af ​​en brøk med det samme antal en ækvivalent brøk. Selvom tallene på de nye fraktioner vil være forskellige, vil de have de samme værdier.
   • Hvis vi f.eks. Tager brøkdelen 4/8 og multiplicerer både tælleren og nævneren med 2, får vi (4 × 2) / (8 × 2) = 8/16. Disse to fraktioner er ækvivalente.
   • (4 × 2) / (8 × 2) er nøjagtigt den samme som 4/8 × 2/2. Husk at når vi multiplicerer to brøker, multiplicerer vi vandret, dvs. tælleren med tælleren og nævneren med nævneren.
   • Bemærk, at 2/2 er lig med 1, når du foretager divisionen. Derfor er det let at se, hvorfor 4/8 og 8/16 er ens, fordi 4/8 × (2/2) stadig er = 4/8. Ligeledes 4/8 = 8/16.
   • Enhver brøkdel har et uendeligt antal ækvivalente fraktioner. Du kan gange tælleren og nævneren med et hvilket som helst heltal, stort eller lille, for at give en ækvivalent brøkdel.

2. 

   
   
   Del tælleren og nævneren med det samme nummer. Ligesom multiplikation bruges division også til at finde en ny brøkdel, der svarer til den oprindelige brøkdel. Del simpelthen tælleren og nævneren af ​​en brøkdel med det samme nummer for at få en tilsvarende brøkdel. Den opnåede brøkdel skal dog have både tælleren og prøven som heltal.
   • Se for eksempel tilbage på fraktionen 4/8. I stedet for at multiplicere deler vi både tælleren og nævneren med 2, vi har (4 ÷ 2) / (8 ÷ 2) = 2/4. 2 og 4 er begge heltal, så denne ækvivalente brøkdel er gyldig.
   reklame

Metode 2 af 5: Brug af grundlæggende multiplikation til bestemmelse af ækvivalens

1. 

   
   
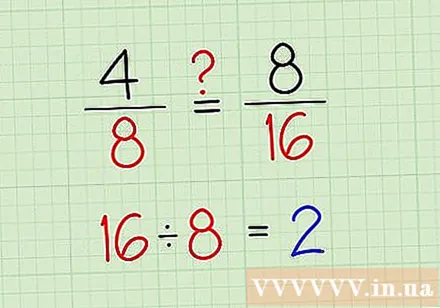
   Find det nummer, hvor den større nævneren ganges med den mindre nævneren. Mange brøkproblemer involverer at bestemme, om to fraktioner er ens eller ikke. Ved at beregne dette tal kan du returnere brøkene til det samme udtryk for at bestemme ækvivalens.
   • Hent f.eks. Fraktionerne 4/8 og 8/16. Den mindre nævneren er 8, og vi bliver nødt til at gange dette tal med 2 for at få den større nævneren på 16. Så det antal, vi skal se efter i dette tilfælde, er 2.
   • For mere komplekse tal skal du bare dele den store nævneren med den lille nævneren. I ovenstående eksempel 16 divideret med 8 er resultatet 2.
   • Dette tal er ikke altid et heltal. For eksempel, hvis nævnerne er 2 og 7, så er 7 divideret med 2 lig med 3,5.

2. 

   
   
   Tælleren og nævneren for fraktionen udtrykkes i det nederste udtryk med tallet identificeret i ovenstående trin. Per definition findes der to forskellige, men ækvivalente fraktioner Tælleren og nævneren er multipla af hinanden. Med andre ord giver multiplikation af tæller og nævneren af ​​en brøk med det samme antal en ækvivalent brøk. Selvom tallene i denne nye fraktion vil være forskellige, er deres værdier de samme.
   • For eksempel, hvis vi tager brøkdelen 4/8 fra trin et og multiplicerer både tælleren og prøven med tallet 2, der er angivet tidligere, har vi (4 × 2) / (8 × 2) = 8/16. Det beviser, at disse to fraktioner er ækvivalente.
   reklame

Metode 3 af 5: Brug af grundlæggende division til at bestemme ækvivalens

1. 

   Del hver brøkdel i en decimal. For enkle brøker uden variabler behøver du kun at repræsentere hver brøk som en decimal for at bestemme ækvivalens. Da hver fraktion i det væsentlige er en division, er dette den enkleste måde at bestemme ækvivalens på.
   • Tag for eksempel brøkdelen 4/8 ovenfor. Fraktionen 4/8 er lig med 4 divideret med 8, 4/8 = 0,5. Du kan dele den brøkdel sådan, 8/16 = 0,5. Uanset brøkternes format er de ækvivalente, hvis de to tal er ens, når de udtrykkes i decimal.
   • Husk, at decimalrepræsentationen kan producere mange cifre, før du konkluderer, at de ikke er ækvivalente. Et grundlæggende eksempel er 1/3 = 0,333… mens 3/10 = 0,3. Bare mere end et ciffer finder vi, at disse to fraktioner ikke er ækvivalente.

2. 

   Del tælleren og nævneren for en brøkdel med det samme nummer for at få en tilsvarende brøkdel. For mere komplekse fraktioner kræver denne opdelingsmetode yderligere trin. Ligesom multiplikation kan du dele tælleren og nævneren af ​​en brøkdel med det samme nummer for at få en ækvivalent brøkdel. Den opnåede brøkdel skal dog have både tælleren og prøven som heltal.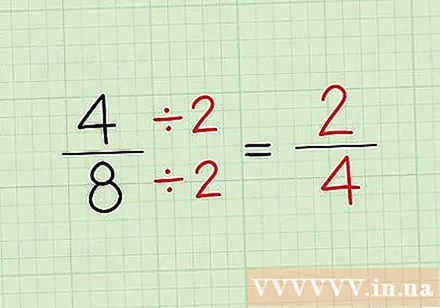
   • Brøkeksempel 4/8. I stedet for at multiplicere er vi det del Både tælleren og nævneren giver 2, vi får (4 ÷ 2) / (8 ÷ 2) = 2/4. 2 og 4 er begge heltal, så denne ækvivalente brøkdel er gyldig.

3. 

   
   
   Reducer fraktionen til sin minimale form. De fleste fraktioner udtrykkes normalt i en minimal form, og du kan returnere dem til deres minimale form ved at dividere med den største fælles faktor i tælleren og prøven. Dette trin fungerer i den samme logik, der repræsenterer ækvivalente fraktioner ved at konvertere dem til den samme nævner, men denne metode kræver reduktion af hver brøk til sin minimale form.
   • Når en brøkdel er i sin minimale form, er tælleren og dens nævneren så lille som muligt. Du kan ikke dele dem med et heltal for at få et mindre tal. For at konvertere en brøk til sin minimale form dividerer vi tælleren og nævneren med største fælles faktor.
   • Den største fælles faktor for tælleren og nævneren er det maksimale antal, de kan deles med. Så i eksemplet 4/8, fordi 4 er det største tal, som både 4 og 8 kan deles med, deler vi tælleren og nævneren af ​​denne brøkdel med 4 for at få den forenklede form. (4 ÷ 4) / (8 ÷ 4) = 1/2. I et andet eksempel 8/16 er GCF 8, resultatet er også 1/2.
   reklame

Metode 4 af 5: Brug af krydsmultiplikation til løsning af variabler Problem

1. 

   
   
   Sæt to fraktioner ens. Vi bruger krydsmultiplikation til problemer, hvor vi ved, at brøker er ækvivalente, men et af tallene er blevet erstattet af variablen (normalt x), som vi skal løse problemet for at finde. I tilfælde som disse er krydsmultiplikation en hurtig metode.

2. 

   
   
   Tag to ækvivalente fraktioner og kryds dem ved hjælp af et "X". Med andre ord multiplicerer du tælleren af ​​en brøkdel med nævneren for den anden og omvendt og sætter derefter disse to resultater ens og løser problemet.
   • Tag to eksempler, 4/8 og 8/16. Disse to fraktioner indeholder ingen variabler, men vi kan bevise, at de er ækvivalente. Ved krydsmultiplikering får vi 4 x 16 = 8 x 8 eller 64 = 64, hvilket naturligvis er korrekt. Hvis de to tal ikke er ens, er fraktionerne ikke ækvivalente.

3. 

   Sæt variablerne i. Da krydsmultiplikation er den nemmeste måde at bestemme ækvivalente brøker, når du skal løse problemet med at finde variabler, skal du tilføje variabler.
   • Overvej f.eks. Følgende ligning 2 / x = 10/13. For at krydse multiplicere multiplicerer vi 2 med 13 og 10 med x og sætter derefter disse to resultater ens:
     • 2 × 13 = 26
     • 10 x x = 10 x
     • 10x = 26. Ved enkle algebraiske metoder kan vi finde variablen x = 26/10 = 2.6, så er de to første ækvivalente fraktioner 2 / 2,6 = 10/13.

4. 

   Brug krydsmultiplikation til ligninger med flere variabler eller variable udtryk. En af de sejeste ting ved krydsmultiplikation er, at uanset om du har to enkle fraktioner (som ovenfor) eller mere komplekse fraktioner, er løsningen nøjagtig den samme. For eksempel, hvis begge fraktioner indeholder variabler, skal du blot fjerne dem i sidste trin i problemløsningsprocessen. Ligeledes, hvis tællere og nævnere for brøker indeholder variable udtryk (såsom x + 1), skal du blot krydse-multiplicere og løse som du normalt ville.
   • Overvej f.eks. Følgende ligning ((x + 3) / 2) = ((x + 1) / 4). Som ovenfor løser vi ved at krydset multiplicere to fraktioner:
     • (x + 3) × 4 = 4x + 12
     • (x + 1) × 2 = 2x + 2
     • 2x + 2 = 4x + 12, træk siderne i 2x
     • 2 = 2x + 12, for at adskille variablen trækker vi siderne til 12
     • -10 = 2x, og del siderne med 2 for at finde x
     • -5 = x
   reklame

Metode 5 af 5: Brug af kvadratisk opløsning til at løse variable ligninger

1. 

   Kryds multiplicer to fraktioner. For ækvivalensproblemer, der kræver brug af kvadratiske løsninger, starter vi stadig med krydsmultiplikation. Enhver krydsmultiplikation involverer imidlertid multiplikation af udtrykket, der indeholder en variabel, med udtrykket, der indeholder en anden variabel, har potentialet til at give et udtryk, der ikke let kan løses ved den algebraiske metode. I tilfælde som disse skal du bruge teknikker som faktorisering og / eller kvadratiske formler.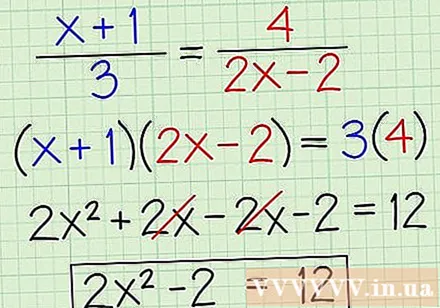
   • Overvej f.eks. Følgende ligning ((x +1) / 3) = (4 / (2x - 2)). Trin 1 krydser vi multiplicere:
     • (x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2
     • 4 × 3 = 12
     • 2x - 2 = 12.

2. 

   Udtryk ligningen som en kvadratisk ligning. Vi skal nu repræsentere ligningen i kvadratisk form (ax + bx + c = 0), hvor vi sætter ligningen til nul. I dette tilfælde trækker vi begge sider med 12 for at få 2x. - 14 = 0.
   • Nogle værdier kan være nul. Selvom 2x - 14 = 0 er den enkleste form for ligning, er dens kvadratiske faktisk 2x + 0x + (-14) = 0. Det hjælper med at reflektere Ret formen af ​​en kvadratisk ligning, selvom nogle værdier er 0.

3. 

   Løs en ligning ved at tilslutte de kendte koefficienter til opløsningsformlen. Den kvadratiske formel (x = (-b +/- √ (b - 4ac)) / 2a) hjælper os med at løse problemet med at finde x på dette tidspunkt. Vær ikke bange, for formlen virker lang. Du skal blot tage værdierne fra den kvadratiske ligning i trin to og udskifte dem i deres respektive positioner inden du løser dem.
   • x = (-b +/- √ (b - 4ac)) / 2a. I ligningen er 2x - 14 = 0, a = 2, b = 0 og c = -14.
   • x = (-0 +/- √ (0 - 4 (2) (- 14))) / 2 (2)
   • x = (+/- √ (0 - -112)) / 2 (2)
   • x = (+/- √ (112)) / 2 (2)
   • x = (+/- 10,58 / 4)
   • x = +/- 2.64

4. 

   Tjek dine svar ved at sætte x tilbage i din kvadratiske ligning. Ved at erstatte den fundne x tilbage i din kvadratiske ligning fra trin to, kan du nemt bestemme, om dit svar er sandt eller falsk. I dette eksempel erstatter du både 2.64 og -2.64 i den originale kvadratiske ligning. reklame

Råd

• Konvertering af brøker til brøker med samme værdi er faktisk formen af ​​at multiplicere dem med 1. Når vi konverterer 1/2 til 2/4, multiplicerer vi faktisk tælleren og nævneren med 2 eller multiplicerer. 1/2 med 2/2, hvilket er lig med 1.
• Om ønsket konverteres det blandede tal til en uregelmæssig brøkdel for at gøre konverteringen lettere. Det er klart, at ikke hver brøkdel, du støder på, er så let at konvertere som vores 4/8 eksempel ovenfor. For eksempel kan blandede tal (for eksempel 1 3/4, 2 5/8, 5 2/3 osv.) Gøre overgangen lidt mere kompliceret. Hvis du har brug for at konvertere et blandet tal til en ækvivalent brøk, kan du gøre det på to måder: konvertere det blandede tal til en uregelmæssig brøk og derefter konvertere som normalt, eller hold det blandede tal og betragt det blandede nummer som svaret.
  • For at konvertere en uregelmæssig brøk skal du multiplicere heltalets del af det blandede tal med nævneren for brøken og derefter tilføje det til tælleren. For eksempel 1 2/3 = ((1 × 3) + 2) / 3 = 5/3. Derefter kan du om ønsket konvertere til ækvivalente fraktioner efter behov. For eksempel 5/3 × 2/2 = 10/6, som stadig er lig med 1 2/3.
  • Vi behøver imidlertid ikke konvertere til den uregelmæssige brøk som ovenfor. Ignorer heltalets del, konverter kun brøkdelen, og tilføj derefter hele taldelen tilbage til den konverterede brøkdel. For eksempel, for 3 4/16 ser vi kun på 4/16. 4/16 & divider; 4/4 = 1/4. Når vi tilføjer heltalets del tilbage, har vi det nye blandede tal 3 1/4.

Advarsel

• Multiplikation og division bruges til at skabe ækvivalente brøker, fordi multiplikation og deling med brøkformen af ​​tallet 1 (2/2, 3/3 osv.) Pr. Definition ikke har nogen indvirkning på brøkværdier. original. Addition og subtraktion gør det ikke.
• Selvom du multiplicerer nævneren og nævneren, når du multiplicerer brøker, kan du ikke tilføje eller trække nævneren, når du tilføjer eller trækker brøker.
  • Som eksemplet ovenfor ser vi, at 4/8 ÷ 4/4 = 1/2. Hvis jeg i stedet plus i 4/4 vil svaret være helt anderledes. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 godt 3/2, intet svar er lig med 4/8.