Indhold

• Trin
• Metode 1 af 3: Del 1: Bestemmelse af bøjningspunktet
• Metode 2 af 3: Beregning af derivater af en funktion
• Metode 3 af 3: Del 3: Find bøjningspunktet
• Tips

I differentialregning er et bøjningspunkt et punkt på en kurve, hvor dets krumning ændrer tegn (fra plus til minus eller fra minus til plus). Dette koncept bruges inden for maskinteknik, økonomi og statistik til at identificere betydelige ændringer i data.

Trin

Metode 1 af 3: Del 1: Bestemmelse af bøjningspunktet

1. 1 Definition af en konkav funktion. Midten af ​​enhver akkord (et segment, der forbinder to punkter) i grafen for en konkav funktion ligger enten under grafen eller på den.
2. 2 Definition af en konveks funktion. Midten af ​​enhver akkord (et segment, der forbinder to punkter) i grafen for en konveks funktion ligger enten over grafen eller på den.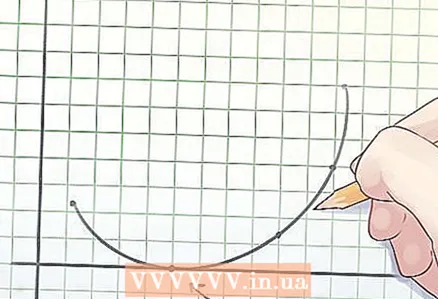
3. 3 Bestemmelse af funktionens rødder. Roden til en funktion er værdien af ​​variablen "x", hvor y = 0.
   • Når du plotter en funktion, er rødderne de punkter, hvor grafen krydser x-aksen.

Metode 2 af 3: Beregning af derivater af en funktion

1. 1 Find den første afledning af funktionen. Se på reglerne for differentiering i lærebogen; du skal lære at tage de første derivater, og først derefter gå videre til mere komplekse beregninger. De første derivater betegnes f '(x). For udtryk for formen ax ^ p + bx ^ (p - 1) + cx + d er det første derivat: apx ^ (p - 1) + b (p - 1) x ^ (p - 2) + c.
   • Find f.eks. Bøjningspunkterne for funktionen f (x) = x ^ 3 + 2x -1. Det første derivat af denne funktion er:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Find den anden afledning af funktionen. Andet derivat er derivatet af det første derivat af den oprindelige funktion. Andet derivat betegnes som f ′ ′ (x).
   • I ovenstående eksempel er det andet derivat:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Sæt det andet derivat til nul, og løse den resulterende ligning. Resultatet bliver det forventede bøjningspunkt.
   • I ovenstående eksempel ser din beregning således ud:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Find den tredje afledning af funktionen. For at kontrollere, at dit resultat faktisk er et bøjningspunkt, skal du finde det tredje derivat, som er derivatet af det andet derivat af den oprindelige funktion. Det tredje derivat betegnes som f ′ ′ ′ (x).
   • I eksemplet ovenfor er det tredje derivat:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Metode 3 af 3: Del 3: Find bøjningspunktet

1. 1 Tjek det tredje derivat. Standardreglen for estimering af et bøjningspunkt er, at hvis det tredje derivat ikke er nul (det vil sige f ′ ′ ′ (x) ≠ 0), så er bøjningspunktet det sande bøjningspunkt. Tjek det tredje derivat; hvis det ikke er nul, så har du fundet det reelle bøjningspunkt.
   • I eksemplet ovenfor er det tredje derivat 6, ikke 0.Så du har fundet det virkelige bøjningspunkt.
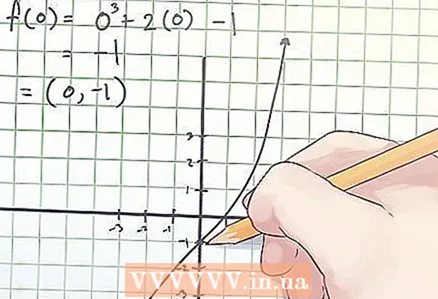2. 2 Find koordinaterne for bøjningspunktet. Bøjningspunktets koordinater er angivet som (x, f (x)), hvor x er værdien af ​​den uafhængige variabel "x" ved bøjningspunktet, f (x) er værdien af ​​den afhængige variabel "y" ved bøjningen punkt.
   • I eksemplet ovenfor fandt du f (0) for at bestemme koordinaterne for bøjningspunktet ved at ligne det andet derivat til nul. Din beregning ser sådan ud:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
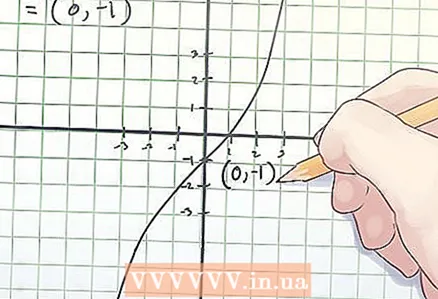3. 3 Skriv koordinaterne for bøjningspunktet ned. Bøjningspunktets koordinater er de fundne x- og f (x) værdier.
   • I ovenstående eksempel er bøjningspunktet ved koordinater (0, -1).

Tips

• Det første derivat af et frit udtryk (primtal) er altid nul.