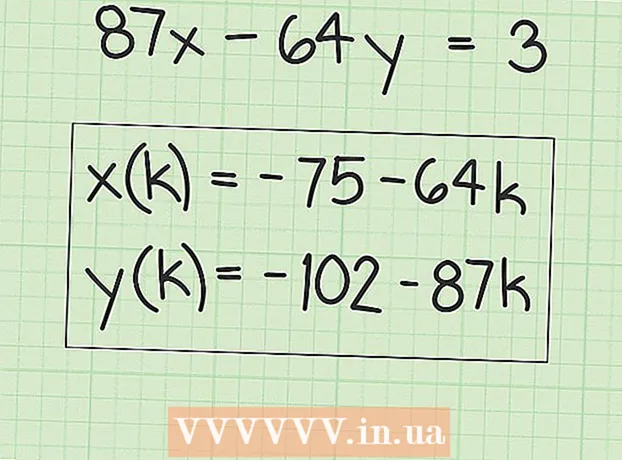
Indhold

• Trin
• Del 1 af 4: Sådan skriver du en ligning
• Del 2 af 4: Sådan skriver du Euklids algoritme
• Del 3 af 4: Sådan finder du en løsning ved hjælp af Euclids algoritme
• Del 4 af 4: Find uendelige andre løsninger

For at løse en lineær Diophantine -ligning skal du finde værdierne for variablerne "x" og "y", som er heltal. En heltal løsning er mere kompleks end normalt og kræver et specifikt sæt handlinger. Først skal du beregne koefficienternes største fælles divisor (GCD) og derefter finde en løsning. Når du har fundet en heltal løsning til en lineær ligning, kan du bruge et simpelt mønster til at finde et uendeligt antal andre løsninger.

Trin

Del 1 af 4: Sådan skriver du en ligning

1. 1 Skriv ligningen ned i standardform. En lineær ligning er en ligning, hvor eksponenterne for variablerne ikke overstiger 1. For at løse en sådan lineær ligning skal du først skrive den i standardform. Standardformen for en lineær ligning ser sådan ud: ${ displaystyle Ax + By = C}$, hvor ${ displaystyle A, B}$ og ${ displaystyle C}$ - hele tal.
   • Hvis ligningen er givet i en anden form, skal du bringe den til standardform ved hjælp af grundlæggende algebraiske operationer. For eksempel givet ligningen ${ displaystyle 23x + 4y -7x = -3y + 15}$... Giv lignende udtryk og skriv ligningen sådan: ${ displaystyle 16x + 7y = 15}$.
2. 2 Forenkle ligningen (hvis det er muligt). Når du skriver ligningen i standardform, skal du se på koefficienterne ${ displaystyle A, B}$ og ${ displaystyle C}$... Hvis disse odds har en GCD, skal du dele alle tre odds med det. Løsningen på en sådan forenklet ligning vil også være løsningen på den oprindelige ligning.
   • For eksempel, hvis alle tre koefficienter er lige, divider dem med mindst 2. For eksempel:
     • ${ displaystyle 42x + 36y = 48}$ (alle medlemmer kan deles med 2)
     • ${ displaystyle 21x + 18y = 24}$ (nu er alle medlemmer delelige med 3)
     • ${ displaystyle 7x + 6y = 8}$ (denne ligning kan ikke længere forenkles)
3. 3 Kontroller, om ligningen kan løses. I nogle tilfælde kan du straks konstatere, at ligningen ikke har nogen løsninger. Hvis koefficienten "C" ikke er delelig med GCD for koefficienterne "A" og "B", har ligningen ingen løsninger.
   • For eksempel hvis begge koefficienter ${ displaystyle A}$ og ${ displaystyle B}$ er lige, så er koefficienten ${ displaystyle C}$ skal være jævn. Men hvis ${ displaystyle C}$ mærkeligt, så er der ingen løsning.
     • Ligningen ${ displaystyle 2x + 4y = 21}$ ingen heltalsløsninger.
     • Ligningen ${ displaystyle 5x + 10y = 17}$ der er ingen heltalsløsninger, da venstre side af ligningen er delelig med 5 og højre side ikke.

Del 2 af 4: Sådan skriver du Euklids algoritme

1. 1 Forstå Euclids algoritme. Det er en række gentagne divisioner, hvor den foregående rest bruges som den næste divisor. Den sidste divisor, der deler tallene integreret, er den største fælles divisor (GCD) af de to tal.
   • Lad os for eksempel finde GCD af tallene 272 og 36 ved hjælp af Euclids algoritme:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Opdel det større tal (272) med det mindre (36) og vær opmærksom på resten (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - divider den forrige divisor (36) med den foregående rest (20). Bemærk den nye rest (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - divider den forrige divisor (20) med den foregående rest (16). Bemærk den nye rest (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Opdel den forrige deler (16) med den foregående rest (4). Da resten er 0, kan vi sige, at 4 er GCD for de to originale tal 272 og 36.
2. 2 Anvend Euclids algoritme på koefficienterne "A" og "B". Når du skriver den lineære ligning i standardform, skal du bestemme koefficienterne "A" og "B" og derefter anvende Euclids algoritme til dem for at finde GCD. For eksempel givet en lineær ligning ${ displaystyle 87x-64y = 3}$.
   • Her er Euclids algoritme for koefficienter A = 87 og B = 64:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Find den største fælles faktor (GCD). Da den sidste divisor var 1, er GCD 87 og 64 1. Således er 87 og 64 primtal i forhold til hinanden.
4. 4 Analyser resultatet. Når du finder gcd -koefficienterne ${ displaystyle A}$ og ${ displaystyle B}$, sammenlign det med koefficienten ${ displaystyle C}$ den originale ligning. Hvis ${ displaystyle C}$ delelig med gcd ${ displaystyle A}$ og ${ displaystyle B}$, ligningen har en heltal løsning; ellers har ligningen ingen løsninger.
   • For eksempel ligningen ${ displaystyle 87x-64y = 3}$ kan løses, fordi 3 er delelig med 1 (gcd = 1).
   • Antag f.eks. GCD = 5. 3 er ikke jævnt delelig med 5, så denne ligning har ingen heltalsløsninger.
   • Som vist nedenfor, hvis en ligning har en heltal løsning, har den også et uendeligt antal andre heltalsløsninger.

Del 3 af 4: Sådan finder du en løsning ved hjælp af Euclids algoritme

1. 1 Nummer trinene til beregning af GCD. For at finde løsningen på en lineær ligning skal du bruge den euklidiske algoritme som grundlag for substitutions- og forenklingsprocessen.
   • Start med at nummerere trinene til beregning af GCD. Beregningsprocessen ser sådan ud:
     • ${ displaystyle { text {Trin 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Trin 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {Trin 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Trin 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Trin 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Trin 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Trin 7}}: 2 = (2 * 1) +0}$
2. 2 Vær opmærksom på det sidste trin, hvor der er en rest. Omskriv ligningen for dette trin for at isolere resten.
   • I vores eksempel er det sidste trin med resten trin 6. Resten er 1. Omskriv ligningen i trin 6 som følger:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Isolér resten af ​​det foregående trin. Denne proces er et trin-for-trin "ryk op". Hver gang vil du isolere resten i ligningen i det foregående trin.
   • Isolér resten af ​​ligningen i trin 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ eller ${ displaystyle 2 = 5-3}$
4. 4 Erstat og forenkle. Bemærk, at ligningen i trin 6 indeholder tallet 2, og i ligningen i trin 5 er tallet 2 isoleret. Så i stedet for “2” i ligningen i trin 6, skal du erstatte udtrykket i trin 5:
   • ${ displaystyle 1 = 3-2}$ (ligning af trin 6)
   • ${ displaystyle 1 = 3- (5-3)}$ (i stedet for 2 blev et udtryk erstattet)
   • ${ displaystyle 1 = 3-5 + 3}$ (åbne parenteser)
   • ${ displaystyle 1 = 2 (3) -5}$ (forenklet)
5. 5 Gentag substitutions- og forenklingsprocessen. Gentag den beskrevne proces og bevæg dig gennem den euklidiske algoritme i omvendt rækkefølge. Hver gang vil du omskrive ligningen fra det foregående trin og tilslutte den til den sidste ligning, du får.
   • Det sidste trin, vi kiggede på, var trin 5. Så gå til trin 4 og isoler resten i ligningen for det trin:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Erstat dette udtryk for "3" i den sidste ligning:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Fortsæt med substitutions- og forenklingsprocessen. Denne proces vil blive gentaget, indtil du når det første trin i den euklidiske algoritme. Målet med processen er at skrive ligningen med koefficienterne 87 og 64 i den originale ligning, der skal løses. I vores eksempel:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (erstattede udtrykket fra trin 3)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (erstattede udtrykket fra trin 2)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (erstattede udtrykket fra trin 1)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Omskriv den resulterende ligning i overensstemmelse med de originale koefficienter. Når du vender tilbage til det første trin i den euklidiske algoritme, vil du se, at den resulterende ligning indeholder to koefficienter for den oprindelige ligning. Omskriv ligningen, så rækkefølgen af ​​dens vilkår matcher koefficienterne i den oprindelige ligning.
   • I vores eksempel, den originale ligning ${ displaystyle 87x-64y = 3}$... Omskriv derfor den resulterende ligning, så koefficienterne bringes på linje.Vær særlig opmærksom på koefficienten "64". I den oprindelige ligning er denne koefficient negativ, og i den euklidiske algoritme er den positiv. Derfor skal faktoren 34 gøres negativ. Den sidste ligning skrives sådan:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Anvend den relevante multiplikator for at finde en løsning. Bemærk, at i vores eksempel er GCD = 1, så slutligningen er 1. Men den oprindelige ligning (87x-64y) er 3. Derfor skal alle termer i den sidste ligning ganges med 3 for at få løsningen:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Skriv heltaleløsningen ned til ligningen. De tal, der ganges med koefficienterne i den oprindelige ligning, er løsningerne til denne ligning.
   • I vores eksempel skriver du løsningen som et par koordinater: ${ displaystyle (x, y) = ( - 75, -102)}$.

Del 4 af 4: Find uendelige andre løsninger

1. 1 Forstå, at der er et uendeligt antal løsninger. Hvis en lineær ligning har en heltal løsning, skal den have uendeligt mange heltal løsninger. Her er et hurtigt bevis (i algebraisk form):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (hvis du tilføjer "B" til "x" og trækker "A" fra "y", ændres værdien af ​​den originale ligning ikke)
2. 2 Registrer de originale x- og y -værdier. Skabelonen til beregning af de næste (uendelige) løsninger starter med den eneste løsning, du allerede har fundet.
   • I vores eksempel er løsningen et par koordinater ${ displaystyle (x, y) = ( - 75, -102)}$.
3. 3 Tilføj "B" -faktoren til "x" -værdien. Gør dette for at finde den nye x -værdi.
   • I vores eksempel x = -75 og B = -64:
     • ${ displaystyle x = -75 + ( - 64) = - 139}$
   • Således er den nye værdi "x": x = -139.
4. 4 Træk "A" -faktoren fra "y" -værdien. For at værdien af ​​den originale ligning ikke ændres, når du tilføjer et tal til "x", skal du trække et andet tal fra "y".
   • I vores eksempel y = -102 og A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Således er den nye værdi for "y": y = -189.
   • Det nye par koordinater vil blive skrevet således: ${ displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Kontroller løsningen. For at kontrollere, at det nye koordinatpar er en løsning på den oprindelige ligning, skal værdierne sættes i ligningen.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Da ligestillingen er opfyldt, er beslutningen korrekt.
6. 6 Skriv udtryk ned for at finde mange løsninger. "X" -værdierne svarer til den originale løsning plus ethvert multiplum af "B" -faktoren. Dette kan skrives som følgende udtryk:
   • x (k) = x + k (B), hvor "x (k)" er sættet med "x" -værdier, og "x" er den oprindelige (første) værdi af "x", som du fandt.
     • I vores eksempel:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), hvor y (k) er mængden af ​​y-værdier og y er den originale (første) y-værdi, du fandt.
     • I vores eksempel:
     • ${ displaystyle y (k) = - 102-87k}$