Indhold

• At træde
• Metode 1 af 3: En første enkle opgave
• Metode 2 af 3: Beregning af den forventede værdi for et specifikt resultat
• Metode 3 af 3: Forstå konceptet
• Tips
• Nødvendigheder

Forventningsværdi er et statistisk udtryk og et begreb, der bruges til at bestemme, hvor nyttigt eller skadeligt en handling vil være. For at beregne den forventede værdi er det nødvendigt at få en god forståelse af hvert resultat i en bestemt situation og den tilknyttede sandsynlighed eller sandsynligheden for, at et bestemt resultat vil forekomme. Trinene nedenfor giver nogle eksempler på øvelser, der hjælper dig med at forstå begrebet forventningsværdi.

At træde

Metode 1 af 3: En første enkle opgave

1. Læs erklæringen. Før du begynder at tænke over alle mulige resultater og sandsynligheder, er det vigtigt, at du forstår problemet. For eksempel et terningespil, der koster € 10 pr. Spil. En hex-matrice rulles en gang, og dine gevinster afhænger af det antal, du ruller. Hvis en 6 rulles, vinder du € 30; en 5 tjener 20 €; ethvert andet tal giver ikke noget.
2. Liste over alle mulige resultater. Det hjælper med at liste alle mulige resultater i en given situation. I eksemplet ovenfor er der 6 mulige resultater. Disse er: (1) kast en 1 og du mister $ 10, (2) kast en 2 og du mister $ 10, (3) kast en 3 og du taber $ 10, (4) kast en 4 og du taber $ 10 , (5) kast en 5 og vind $ 10, (6) kast en 6 og vind $ 20.
   • Bemærk, at hvert resultat er 10 € mindre end beskrevet ovenfor, da du først skal betale 10 € pr. Spil uanset resultatet.
3. Bestem sandsynligheden for hvert resultat. I dette tilfælde er sandsynligheden for 6 udfald den samme. Sandsynligheden for, at et tilfældigt tal rulles, er 1 ud af 6. For at gøre det lettere at nedskrive skriver vi brøken (1/6) som en decimal ved hjælp af en lommeregner: 0,167. Skriv denne sandsynlighed ved siden af ​​hvert resultat, især hvis du vil løse et problem med forskellige sandsynligheder for hvert resultat.
   • Din 1/6 lommeregner kan muligvis tjene noget som 0.166667. Vi afrunder dette til 0,167 for at gøre det lettere at beregne uden at ofre nøjagtigheden.
   • Hvis du vil have et meget nøjagtigt resultat, skal du ikke gøre det til et decimal, bare indtast 1/6 i formlen og beregne det på din lommeregner.
4. Registrer værdien af ​​hvert resultat. Multiplicer $ et resultat med sandsynligheden for, at resultatet opstår for at beregne, hvor mange penge resultatet vil bidrage til den forventede værdi. For eksempel er resultatet af at rulle en 1 - $ 10, og sandsynligheden for at rulle en 1 er 0,167. Værdien af ​​at kaste en 1 er derfor (-10) * (0,167).
   • Det er ikke nødvendigt at beregne disse resultater nu, hvis du har en lommeregner, der kan udføre flere operationer på samme tid. Du får et mere præcist resultat, hvis du indtaster hele ligningen.
5. Tilføj værdien af ​​hvert resultat for at få den forventede værdi af en begivenhed. For at fortsætte med ovenstående eksempel er terningespilets forventningsværdi: (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (10 * 0.167) + (20 * 0.167) eller - € 1.67. Så du kan forvente at tabe $ 1,67 hver gang på dette spil (pr. Spil).
6. Hvad er konsekvenserne af at beregne den forventede værdi. I eksemplet ovenfor bestemte vi, at det forventede overskud (tab) ville være - € 1,67 pr. Kast. Dette er et umuligt resultat for 1 spil; du kan miste 10 €, vinde 10 € eller vinde 20 €. Men på lang sigt er den forventede værdi en nyttig gennemsnitlig sandsynlighed. Hvis du fortsætter med at spille dette spil, mister du i gennemsnit ca. $ 1,67 pr. Spil. En anden måde at tænke på den forventede værdi er ved at tildele spillet visse omkostninger (eller fordele); du skal kun spille dette spil, hvis du finder det det værd, nyd det nok til at bruge $ 1,67 på det hver gang.
   • Jo oftere en situation gentages, jo mere nøjagtigt er den forventede værdi en repræsentation af det faktiske gennemsnitlige resultat. For eksempel, måske spiller du spillet 5 gange i træk, og du taber hver gang, hvilket resulterer i et gennemsnitligt tab på $ 10. Men hvis du spiller spillet 1000 gange mere, kommer det gennemsnitlige resultat tættere og tættere på den forventede værdi på - € 1,67 pr. Spil. Dette princip kaldes "loven om stort antal".

Metode 2 af 3: Beregning af den forventede værdi for et specifikt resultat

1. Brug denne metode til at beregne det gennemsnitlige antal mønter, du skal vende, før et bestemt mønster opstår. For eksempel kan du bruge metoden til at finde ud af det forventede antal mønter, der skal vendes, indtil du har hoveder to gange i træk. Dette problem er lidt vanskeligere end et standardproblem med forventningsværdier, så læs først ovenstående del af denne artikel, hvis du ikke er bekendt med begrebet forventningsværdi.
2. Antag, at vi leder efter en værdi x. Du prøver at bestemme, hvor mange mønter du skal vende i gennemsnit for at få to hoveder i træk. Vi foretager nu en sammenligning for at finde svaret. Vi kalder det svar, vi leder efter x. Vi foretager den nødvendige sammenligning trin for trin. Vi har i øjeblikket følgende:
   • x = ___
3. Tænk over, hvad der sker, hvis den første flip producerer en mønt. Dette vil være tilfældet i halvdelen af ​​tilfældene. Hvis dette er tilfældet, har du "spildt" en roll over, mens chancen for at rulle et hoved to gange i træk ikke har ændret sig. Som med møntkastet forventes det, at du skal kaste et gennemsnitligt antal gange, før du får et hoved to gange i træk. Med andre ord ville du forvente at rulle et x antal gange plus dem, du allerede har spillet. I form af en ligning:
   • x = (0,5) (x + 1) + ___
   • Vi skal udfylde det tomme rum, når vi fortsætter med at tænke på andre situationer.
   • Du kan bruge brøker i stedet for decimaler, hvis det er lettere eller nødvendigt.
4. Tænk over, hvad der sker, når du kaster hovedet. Der er en 0,5 (eller 1/2) chance for, at du kaster en kop første gang. Dette ser ud til at komme tættere på målet om at kaste et hoved to gange i træk, men hvor meget? Den nemmeste måde at finde ud af er at tænke over dine muligheder på anden runde:
   • Hvis det andet kast er en mønt, er vi tilbage til starten.
   • Hvis anden gang også er en kop, så er vi færdige!
5. Lær hvordan du beregner sandsynligheden for, at to begivenheder begge vil forekomme. Vi ved nu, at du har 50% chance for, at du kaster en kop, men hvad er chancen for, at du vil kaste en kop to gange i træk? For at beregne denne sandsynlighed skal du gange sandsynligheden for begge. I dette tilfælde er det 0,5 x 0,5 = 0,25. Selvfølgelig er dette også chancen for, at du vil rulle hoveder og derefter haler, fordi de begge har en chance for, at 0,5 opstår: 0,5 x 0,5 = 0,25.
6. Tilføj resultatet for "hoveder, derefter haler" til ligningen. Nu hvor vi har beregnet sandsynligheden for, at denne begivenhed vil forekomme, kan vi gå videre til at udvide ligningen. Der er en 0,25 (eller 1/4) chance for at vi spilder kast to gange uden at bevæge os fremad. Men nu har vi stadig brug for et x antal flere kast i gennemsnit for at få det resultat, vi ønsker at få, plus de 2, vi allerede har kastet. I ligningsform bliver dette til (0,25) (x + 2), som vi nu kan tilføje til ligningen:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + ___
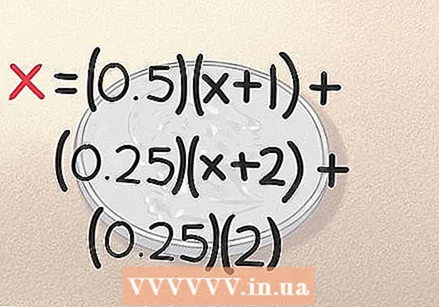7. Tilføj resultatet for "overskrift, overskrift" til ligningen. Hvis du ruller hovedet, skal du gå med de to første kast af mønterne, så er du færdig. Du fik resultatet i nøjagtigt 2 kast. Som vi bemærkede tidligere, er der en 0,25 chance for at dette sker, så ligningen for dette er (0,25) (2). Vores sammenligning er nu afsluttet:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + (0,25) (2)
   • Hvis du ikke er sikker på, at du har gennemgået alle mulige situationer, er der en nem måde at kontrollere, at ligningen er komplet. Det første tal i hver del af ligningen repræsenterer sandsynligheden for, at en begivenhed vil forekomme. Dette tilføjer altid op til 1. Her er 0,5 + 0,25 + 0,25 = 1, så vi ved, at vi har inkluderet enhver situation.
8. Forenkle ligningen. Lad os gøre ligningen lidt lettere ved at multiplicere. Husk, at hvis du ser noget i parentes som dette: (0.5) (x + 1), multiplicerer du 0,5 med hvert udtryk, der er i det andet sæt parenteser. Dette giver dig følgende: 0,5x + (0,5) (1) eller 0,5x + 0,5. Lad os gøre dette for hvert udtryk i ligningen, og kombiner derefter disse termer, så det hele ser lidt enklere ud:
   • x = 0,5x + (0,5) (1) + 0,25x + (0,25) (2) + (0,25) (2)
   • x = 0,5x + 0,5 + 0,25x + 0,5 + 0,5
   • x = 0,75x + 1,5
9. Løs til x. Som i enhver ligning skal du isolere x på den ene side af ligningen for at beregne den. Husk, x betyder "det gennemsnitlige antal mønter, du skal kaste for at få hoveder to gange i træk." Når vi har beregnet x, har vi også fundet vores svar.
   • x = 0,75x + 1,5
   • x - 0,75x = 0,75x + 1,5 - 0,75x
   • 0,25x = 1,5
   • (0,25x) / (0,25) = (1,5) / (0,25)
   • x = 6
   • I gennemsnit skal du kaste en mønt 6 gange, før du kaster hoveder to gange.

Metode 3 af 3: Forstå konceptet

1. Hvad er en forventet værdi faktisk. Forventningsværdien er ikke nødvendigvis det mest oplagte eller logiske resultat. Nogle gange kan en forventningsværdi endda være en umulig værdi i en given situation. For eksempel kan forventningsværdien være + € 5 for et spil med en gevinst på højst € 10. Hvad forventningsværdien indikerer er, hvor meget værdi en bestemt begivenhed har. Hvis et spil har en forventet værdi på + € 5, kan du spille det, hvis du føler, det er værd at den tid og de penge, du kan få pr. Spil. Hvis et andet spil har en forventet værdi på - $ 20, så spiller du det kun, hvis du mener, at hvert spil er $ 20 værd.
2. Forstå begrebet uafhængige begivenheder. I hverdagen tror mange af os, at vi har en heldig dag, når der sker nogle gode ting, og vi forventer, at resten af ​​dagen går den vej.På samme måde kan vi tro, at vi har fået nok af en ulykke, og at der virkelig skal gøres noget sjovt nu. Matematisk går ting ikke sådan. Hvis du kaster en almindelig mønt, er der nøjagtig den samme chance for at du kaster et hoved eller en mønt. Det betyder ikke noget, hvor mange gange du allerede har kastet; næste gang du smider, fungerer det stadig på samme måde. Møntkastet er "uafhængigt" af de andre kast, det påvirkes ikke af det.
   • Troen på, at du kan være heldig eller uheldig, når du kaster mønter (eller ethvert andet hasardspil), eller Det faktum, at alt dit uheld nu er afsluttet, og heldet er på din side, kaldes også gambler snyderi (eller gamblerens fejlslutning). Dette har at gøre med folks tendens til at træffe risikable eller dumme beslutninger, når de føler, at lykken er på deres side, eller hvis de føler sig "heldige striber", eller hvis de føler, at deres "held er ved at vende." "
3. Forstå loven i stort antal. Du tror måske, at forventningsværdien ikke rigtig er nyttig, fordi den kun sjældent fortæller dig, hvad det faktiske resultat af en situation er. Hvis du har beregnet, at den forventede værdi af et roulette-spil er - € 1, og du spiller spillet 3 gange, ender du som regel med - € 10 eller + € 60 eller et andet resultat. "Loven om store tal" hjælper med at forklare, hvorfor forventningsværdien er mere nyttig, end du måske tror: jo mere du spiller, jo tættere på forventningsværdien vil det gennemsnitlige resultat være. Når man ser på det store antal begivenheder, er der en god chance for, at det endelige resultat er tæt på den forventede værdi.

Tips

• I de situationer, hvor flere resultater er mulige, kan du oprette et regneark på computeren for at beregne den forventede værdi ved hjælp af resultaterne og deres sandsynligheder.
• Ovenstående € -beregninger fungerer også i andre valutaer.

Nødvendigheder

• Blyant
• Papir
• Lommeregner