Indhold

• Trin
• Råd

Hvis du er en matematiker eller en grafisk programmør, bliver du sandsynligvis nødt til at finde vinklen mellem to givne vektorer. I denne artikel viser wikiHow dig, hvordan du gør netop det.

Trin

Del 1 af 2: Find vinklen mellem to vektorer

1. 

   Vektor definition. Skriv alle oplysninger om de to vektorer, du har, ned. Antag at du kun har de angivne parametre for deres dimensionelle koordinater (også kaldet komponenter). Hvis du allerede kender længden (størrelsen) af en vektor, kan du springe nogle af nedenstående trin over.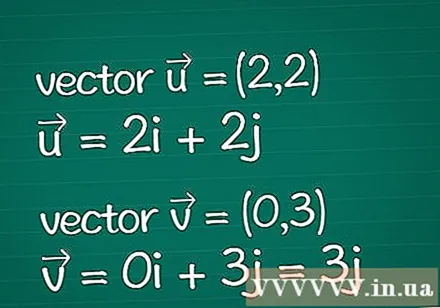
   • Eksempel: To-dimensionel vektor = (2,2) og to-dimensionel vektor = (0,3). De kan også skrives som = 2jeg + 2j og = 0jeg + 3j = 3j.
   • Selvom to-dimensionelle vektorer bruges i eksemplet i denne artikel, kan følgende instruktioner gælde for vektorer med et vilkårligt antal dimensioner.

2. 

   
   
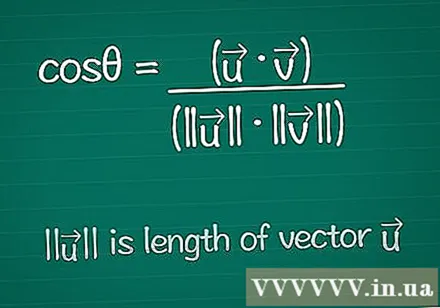
   Skriv cosinusformlen ned. For at finde vinklen θ mellem to vektorer starter vi med formlen til at finde cosinus til den vinkel. Du kan lære om denne formel nedenfor eller bare skrive den ned sådan:
   • cosθ = (•) / (|||| ||||)
   • |||| betyder "vektorens længde".
   • • er det skalære produkt fra de to vektorer - dette forklares nedenfor.

3. 

   
   
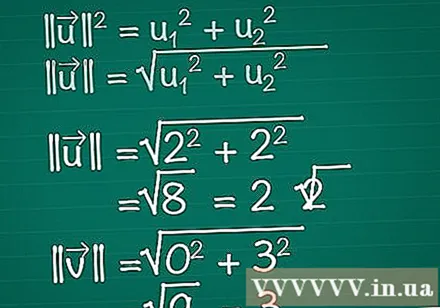
   Beregn længden af ​​hver vektor. Forestil dig, at en højre trekant består af x-, y-komponenterne i vektoren og selve vektoren. Vektoren danner hypotenusen i trekanten, så for at finde dens længde bruger vi den pythagoriske sætning. Faktisk kan denne formel let udvides til en vektor med et hvilket som helst antal dimensioner.
   • || u || = u₁ + u₂. Hvis en vektor har mere end to elementer, skal du bare fortsætte med at tilføje + u₃ + u₄ +...
   • Derfor for en to-dimensionel vektor, || u || = √ (u₁ + u₂).
   • I dette eksempel, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
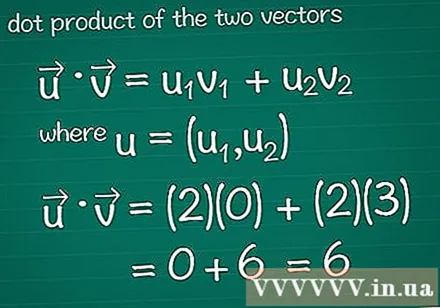
   Beregn det skalære produkt af to vektorer. Måske har du lært metoden til vektormultiplikation, også kendt som skalar det her. For at beregne det skalære produkt i forhold til deres sammensætning skal du multiplicere ingredienserne i hver retning sammen og derefter tilføje hele resultatet.
   • For grafikprogrammet henvises til Tip, før du læser videre.
   • I matematik • = u₁v₁ + u₂v₂, hvor, u = (u₁, u₂). Hvis vektoren har mere end to elementer, skal du blot tilføje + u₃v₃ + u₄v₄...
   • I dette eksempel er • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dette er det skalære produkt af vektoren og vektoren.

5. 

   Sæt resultaterne i formlen. Husk at cosθ = (•) / (|||| || ||). Nu kender vi både det skalære produkt og længden af ​​hver vektor. Indtast disse i formlen for at beregne vinkelens cosinus.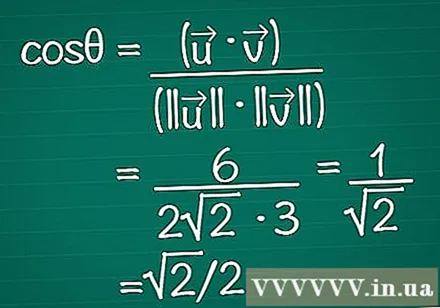
   • I vores eksempel er cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Find vinklen ud fra dens cosinus. Du kan bruge arccos eller cos-funktionen i en lommeregner til at finde θ fra en kendt cos-værdi. Med nogle resultater kan du muligvis finde vinklen baseret på enhedens cirkel.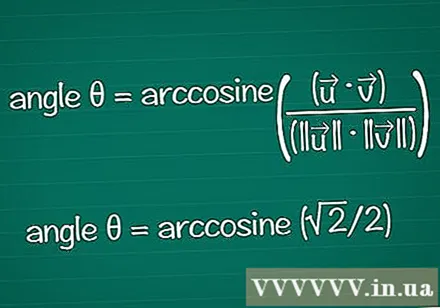
   • I eksemplet er cosθ = √2 / 2. Indtast "arccos (√2 ​​/ 2)" i din lommeregner for at finde vinklen. Eller du kan finde vinklen θ på enhedens cirkel i position cosθ = √2 / 2. Det gælder for θ = /₄ eller 45º.
   • Når man kombinerer alt, er den endelige formel: vinkel θ = arccosine ((•) / (|||| || ||))
   reklame

Del 2 af 2: Bestemmelse af vinkelformlen

1. 

   Forstå formålet med formlen. Denne formel blev ikke afledt af eksisterende regler. I stedet er det dannet som definitionen af ​​det skalære produkt og vinklen mellem de to vektorer. Alligevel var det ikke en vilkårlig beslutning. Når vi går tilbage til grundlæggende geometri, kan vi forstå, hvorfor denne formel giver intuitive og nyttige definitioner.
   • Eksemplerne nedenfor bruger todimensionelle vektorer, fordi de er nemmeste at forstå og enkleste. Tredimensionelle eller flere vektorer har egenskaber defineret af næsten ens generelle formler.

2. 

   Gennemgå Cosines sætning. Overvej en almindelig trekant med vinkel θ mellem siderne a og b, modsatte side c. Cosine sætningen siger, at c = a + b -2abcos(θ). Dette resultat hentes ganske enkelt fra grundlæggende geometri.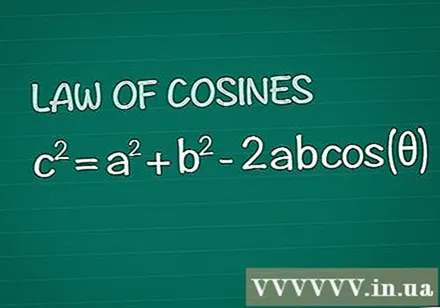

3. 

   Forbind to vektorer, der danner en trekant. Tegn et par to-dimensionelle vektorer på papir, vektorer og vektorer, hvor θ er vinklen mellem dem. Tegn en tredje vektor mellem disse to for at oprette en trekant. Med andre ord, tegne en vektor sådan at + =. Vektor = -.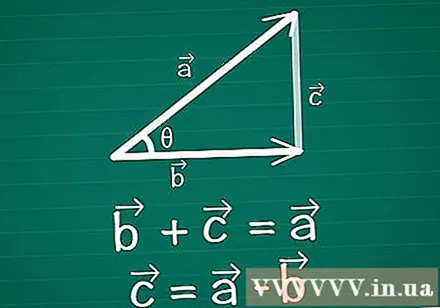

4. 

   Skriv Cosinus sætning til denne trekant. Udskift sidelængden af ​​vores "vektortrekant" i Cosine-sætningen:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Omskriv med skalarprodukt. Husk, at et skalarprodukt er billedet af den ene vektor på den anden. Det skalære produkt af en vektor med sig selv kræver ingen projektion, for her er der ingen forskel i retning. Det betyder • = || a ||. Ved hjælp af dette omskriver vi ligningen:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Omskrevet den samme formel med succes. Udvid venstre side af formlen, og forenk derefter for at få formlen brugt til at finde vinkler.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   reklame

Råd

• For at ændre værdier og løse problemet hurtigt, brug denne formel til ethvert par to-dimensionelle vektorer: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Hvis du arbejder med computergrafiksoftware, er chancerne for, at du kun skal være opmærksom på vektordimensionen uden at bekymre dig om deres længde. Brug følgende trin til at forkorte en ligning og fremskynde dit program:
  • Normaliser hver vektor, så de er lig med 1. For at gøre dette skal du dele hver af vektorkomponenterne med dens længde.
  • Få det normaliserede produkt af skalaren i stedet for den oprindelige vektor.
  • Da længden er 1, kan vi udelukke længdeelementerne fra ligningen. Endelig er den opnåede vinkelligning arccos (•).
• Baseret på cosinusformlen kan vi hurtigt bestemme, om vinklen er spids eller stump. Start med cosθ = (•) / (|||| ||||):
  • Venstre og højre side af ligningen skal have det samme tegn (positiv eller negativ).
  • Da længden altid er positiv, skal cosθ have det samme tegn som det skalære produkt.
  • Derfor, hvis produktet er positivt, er cosθ også positivt. Vi er i den første kvadrant af enhedens cirkel med θ <π / 2 eller 90º. Vinklen at finde er den skarpe vinkel.
  • Hvis det skalære produkt er negativt, er cosθ negativt. Vi befinder os i den anden kvadrant af enhedscirklen med π / 2 <θ ≤ π eller 90º <θ ≤ 180º. Det er fængselshjørnet.