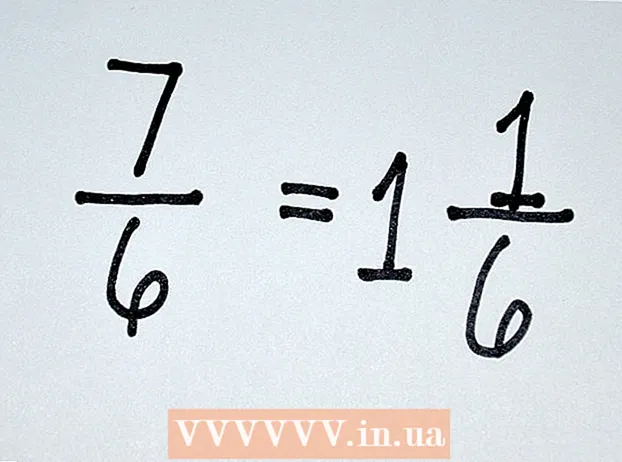
Indhold

• At træde
• Metode 1 af 2: Opret ækvivalente fraktioner
• Metode 2 af 2: Løsning af ækvivalente fraktioner med variabler
• Tips
• Advarsler

To fraktioner er "ækvivalente", hvis de har den samme værdi. For eksempel er fraktionerne 1/2 og 2/4 ækvivalente, fordi 1 divideret med 2 har den samme værdi som 2 divideret med 4 (0,5 i decimalform). At vide, hvordan man konverterer en brøk til en anden, men tilsvarende brøk, er en væsentlig matematisk værdighed, du har brug for, fra grundlæggende algebra til raketvidenskab. Se trin 1 for at komme i gang!

At træde

Metode 1 af 2: Opret ækvivalente fraktioner

1. Multiplicer tælleren og nævneren af ​​en brøkdel med det samme nummer for at få en ækvivalent brøkdel. To fraktioner, der er forskellige, men som pr. Definition er ækvivalente, tællere og nævnere, der er multipla af hinanden. Med andre ord multiplicerer tælleren og nævneren af ​​en brøk med det samme tal en ækvivalent brøk. Selvom tallene i denne nye fraktion er forskellige, har den stadig den samme værdi.
   • Hvis vi for eksempel tager brøkdelen 4/8 og ganger både tælleren og nævneren med 2, får vi (4 × 2) / (8 × 2) = 8/16. Disse to fraktioner er ækvivalente.
     • (4 × 2) / (8 × 2) er i det væsentlige den samme som 4/8 × 2 / 2. Husk at multiplicere to brøker er sådan her - tæller gange tæller og nævneren gange nævneren. Bemærk, at 2/2 er lig med 1. Så det er let at se, hvorfor 4/8 er lig med 8/16 - den anden brøkdel er den første brøk multipliceret med 2!
2. Del tælleren og nævneren eller en brøkdel med det samme nummer for at få en ækvivalent brøkdel. Ligesom multiplikation kan division også bruges til at finde en ny brøkdel, der svarer til den givne brøkdel. Del simpelthen tælleren og nævneren af ​​en brøkdel med det samme nummer for at få en tilsvarende brøkdel. Der er en fangst her - den resulterende brøk skal bestå af heltal i både tælleren og nævneren for at være gyldig.
   • Lad os for eksempel tage 4/8 igen. Hvis vi i stedet for en multiplikation deler både tælleren og nævneren med 2, får vi (4 ÷ 2) / (8 ÷ 2) = 2/4. 2 og 4 er begge hele tal, så denne ækvivalente brøkdel er gyldig.
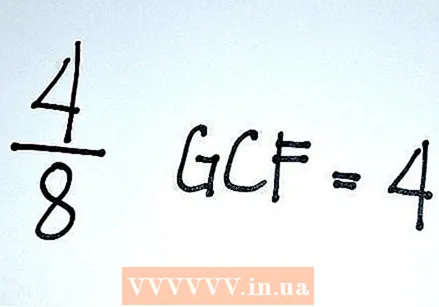3. Forenkle din brøk ved hjælp af den største fælles divisor (GCD). Enhver given brøk har et uendeligt antal ækvivalente brøker - du kan gange tæller og nævner med ethvert heltal, stort eller lille for at få en tilsvarende brøkdel. Men den enkleste form for en given brøkdel er normalt den med de mindste udtryk. I så fald er tælleren og nævneren begge så små som muligt - de kan ikke længere deles med noget heltal for at gøre udtrykket endnu mindre. For at forenkle en brøkdel deler vi både tælleren og nævneren med største fællesnævner.
   • Tællerens og nævnerens største fælles divisor (GGD) er det største heltal, således at både tæller og nævner kan deles. Så i vores 4/8 eksempel, fordi 4 er den største skiller på både 4 og 8, deler vi tælleren og nævneren af ​​vores brøkdel med 4 for at få de enkleste termer. (4 ÷ 4) / (8 ÷ 4) = 1/2.
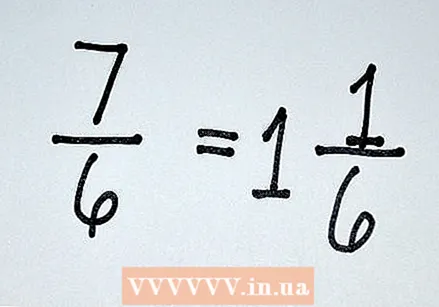4. Om ønsket konverteres blandede tal til ukorrekte brøker for at gøre konvertering lettere. Selvfølgelig vil ikke hver brøkdel, du støder på, give mening lige så let som 4/8. For eksempel kan blandede tal (f.eks. 1 3/4, 2 5/8, 5 2/3 osv.) Gøre denne konvertering lidt vanskeligere.Hvis du vil lave en brøkdel af et blandet tal, kan du gøre dette på to måder: Gør det blandede tal til en forkert brøkdel, og fortsæt derefter, eller hold det blandede tal og giv et blandet tal som svar.
   • For at konvertere en forkert brøk skal du multiplicere heltalet med det blandede tal med nævneren for brøken og derefter tilføje produktet til tælleren. For eksempel 1 2/3 = ((1 × 3) + 2) / 3 = 5/3. Så kan du konvertere dette igen, hvis det er nødvendigt. For eksempel 5/3 × 2/2 = 10/6, stadig det samme som 1 2/3.
   • Imidlertid er det ikke nødvendigt at konvertere en forkert brøkdel. Vi kan ignorere hele tallet og bare konvertere brøken og derefter tilføje hele tallet til det. For eksempel ved 3 4/16 ser vi kun på 4/16. 4/16 ÷ 4/4 = 1/4. Så nu tilføjer vi hele nummeret igen og får et nyt blandet tal, 3 1/4.
5. Aldrig tilføje eller trække for at få ækvivalente brøker. Når du konverterer brøker til deres ækvivalente form, er det vigtigt at huske, at de eneste operationer, du anvender, er multiplikation og division. Brug aldrig addition eller subtraktion. Multiplikation og division arbejder for at få ækvivalente brøker, fordi disse operationer faktisk er former for tallet 1 (2/2, 3/3 osv.) Og giver svar svarende til den brøk, du startede med. Addition og subtraktion har ikke denne mulighed.
   • For eksempel ovenfor fandt vi, at 4/8 ÷ 4/4 = 1/2. Hvis vi i stedet tilføjede 4/4 til dette, ville vi have fået et helt andet svar. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 eller 3/2, og ingen af ​​disse er lig med 4/8.

Metode 2 af 2: Løsning af ækvivalente fraktioner med variabler

1. Brug krydsmultiplikation til at løse ækvivalensproblemer med brøker. En vanskelig type algebra-problem, der beskæftiger sig med ækvivalente brøker, involverer ligninger med to brøker, hvor den ene eller begge indeholder en variabel. I tilfælde som dette ved vi, at disse fraktioner er ækvivalente, fordi de er de eneste udtryk på hver side af ligningstegnet på en ligning, men det er ikke altid indlysende, hvordan man løser for variablen. Heldigvis med krydsmultiplikation kan vi løse denne type problemer uden problemer.
   • Korsmultiplikation er bare, hvad det lyder som - du multiplicerer på tværs over lighedstegnet. Med andre ord multiplicerer du tælleren af ​​en brøkdel med nævneren for den anden brøkdel og omvendt. Så løser du ligningen yderligere.
   • For eksempel har vi ligningen 2 / x = 10/13. Kryds multiplicer nu: multiplicer 2 med 13 og 10 med x, og udarbejd ligningen yderligere:
     • 2 × 13 = 26
     • 10 × x = 10 x
     • 10x = 26. Nu udarbejder vi ligningen yderligere. x = 26/10 = 2.6
2. Brug krydsmultiplikation på samme måde som sammenligning med flere variabler eller variable udtryk. En af de bedste egenskaber ved krydsmultiplikation er, at det fungerer meget det samme, uanset om du har at gøre med to enkle eller komplekse fraktioner. For eksempel, hvis begge fraktioner indeholder variabler, ændres intet - du skal bare annullere disse variabler. Ligeledes, hvis tællerne eller nævnerne for dine brøker indeholder variable udtryk, skal du bare "fortsætte med at multiplicere" ved hjælp af den distribuerende egenskab og løsning, som du normalt gør.
   • Antag for eksempel, at vi har ligningen ((x + 3) / 2) = ((x + 1) / 4). I dette tilfælde løser vi det med krydsmultiplikation:
     • (x + 3) × 4 = 4x + 12
     • (x + 1) × 2 = 2x + 2
     • 2x + 2 = 4x + 12
     • 2 = 2x + 12
     • -10 = 2x
     • -5 = x
3. Brug polynomiske løsningsteknikker. Krydsmultiplikation betyder ikke noget altid et resultat, som du kan løse med simpel algebra. Hvis du har at gøre med variable udtryk, får du hurtigt en andengradsligning eller andet polynom som resultat. I sådanne tilfælde bruger du f.eks. Kvadrering og / eller kvadratformlen.
   • For eksempel tager vi ligningen ((x +1) / 3) = (4 / (2x - 2)). Første kryds ganges:
     • (x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2
     • 4 × 3 = 12
     • 2x - 2 = 12. På dette tidspunkt vil vi konvertere dette til en andengrads ligning (ax + bx + c = 0) ved at trække 12 fra begge sider, hvilket giver os 2x - 14 = 0. Nu bruger vi formlen (x = (-b +/- √ (b - 4ac)) / 2a) for at finde værdien af ​​x:
       • x = (-b +/- √ (b - 4ac)) / 2a. I vores ligning er 2x - 14 = 0, a = 2, b = 0 og c = -14.
       • x = (-0 +/- √ (0 - 4 (2) (- 14))) / 2 (2)
       • x = (+/- √ (0 - -112)) / 2 (2)
       • x = (+/- √ (112)) / 2 (2)
       • x = (+/- 10,58 / 4)
       • x = +/- 2.64 På dette tidspunkt kontrollerer vi vores svar ved at erstatte 2.64 og -2.64 i den oprindelige andengradsligning.

Tips

• Konvertering af brøker til en ækvivalent form er grundlæggende det samme som at gange med en brøk som 2/2 eller 5/5. Da dette i sidste ende er lig med 1, forbliver værdien af ​​fraktionen den samme.

Advarsler

• Addition og subtraktion af fraktioner er forskellig fra multiplikation og division af fraktioner.