Indhold

• Trin
• Metode 1 af 5: Terminologi
• Metode 2 af 5: Undersøg problemformuleringen
• Metode 3 af 5: Findning af enhedsvektoren
• Metode 4 af 5: Sådan normaliseres en vektor i 2-dimensionelt rum
• Metode 5 af 5: Sådan normaliseres en vektor i n-dimensionelt rum

En vektor er et geometrisk objekt, det er kendetegnet ved retning og størrelse. Det kan repræsenteres som et linjesegment med et udgangspunkt i den ene ende og en pil i den anden, mens længden af ​​segmentet svarer til vektorens størrelse, og pilen angiver dens retning. Vektornormalisering er en standardoperation i matematik; i praksis bruges den i computergrafik.

Trin

Metode 1 af 5: Terminologi

1. 1 Lad os definere en enhedsvektor. En enhedsvektor af vektor A er en vektor, hvis retning falder sammen med retningen for vektor A, og længden er 1. Det kan strengt bevises, at hver vektor har en og kun en enhedsvektor, der svarer til den.
2. 2 Lær hvad vektor normalisering er. Dette er proceduren for at finde enhedsvektoren for en given vektor A.
3. 3 Lad os definere en tilsluttet vektor. I et kartesisk koordinatsystem går den tilhørende vektor fra oprindelsen, det vil sige for det 2-dimensionelle tilfælde fra punktet (0,0). Dette gør det muligt for vektoren kun at blive specificeret af koordinaterne for dets slutpunkt.
4. 4 Lær at skrive vektorer. Hvis vi begrænser os til tilsluttede vektorer, peger i notationen A = (x, y) koordinatparet (x, y) til slutpunktet for vektoren A.

Metode 2 af 5: Undersøg problemformuleringen

1. 1 Fastslå, hvad der er kendt. Fra definitionen af ​​en enhedsvektor ved vi, at denne vektors udgangspunkt og retning falder sammen med de analoge egenskaber ved vektor A. Desuden er enhedsvektorens længde 1.
2. 2 Find ud af, hvad du skal finde. Det er påkrævet at finde koordinaterne for enhedsvektorens slutpunkt.

Metode 3 af 5: Findning af enhedsvektoren

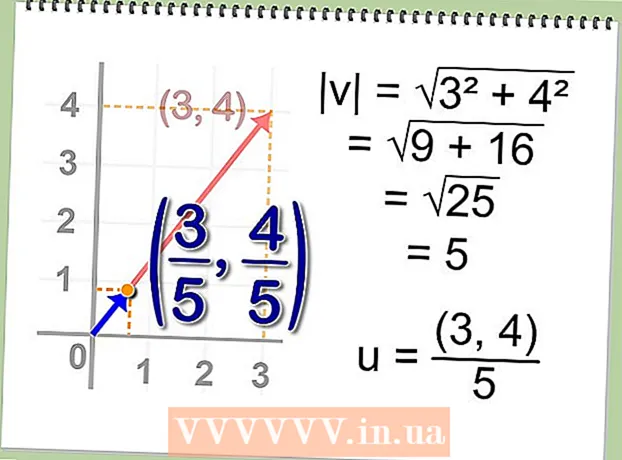
• Find slutpunktet for enhedsvektoren for vektor A = (x, y). Enhedsvektoren og vektor A danner lignende retvinklede trekanter, så enhedsvektorens slutpunkt vil have koordinater (x / c, y / c), hvor du skal finde c. Derudover er enhedsvektorens længde 1. Således har vi ifølge Pythagoras sætning: [x ^ 2 / c ^ 2 + y ^ 2 / c ^ 2] ^ (1/2) = 1 -> [(x ^ 2 + y ^ 2) / c ^ 2] ^ (1/2) -> (x ^ 2 + y ^ 2) ^ (1/2) / c = 1 -> c = (x ^ 2 + y ^ 2) ^ (1/2). Det vil sige, at enhedsvektoren i vektoren A = (x, y) er givet ved udtrykket u = (x / (x ^ 2 + y ^ 2) ^ (1/2), y / (x ^ 2 + y ^ 2) ^ (1/2)).

Metode 4 af 5: Sådan normaliseres en vektor i 2-dimensionelt rum

• Antag, at vektor A starter ved oprindelsen og slutter ved (2,3), det vil sige A = (2,3). Find enhedsvektoren: u = (x / (x ^ 2 + y ^ 2) ^ (1/2), y / (x ^ 2 + y ^ 2) ^ (1/2)) = (2 / (2 ^ 2 + 3 ^ 2) ^ (1/2), 3 / (2 ^ 2 + 3 ^ 2) ^ (1/2)) = (2 / (13 ^ (1/2)), 3 / (13 ^ (1/2))). Således fører normaliseringen af ​​vektoren A = (2,3) til vektoren u = (2 / (13 ^ (1/2)), 3 / (13 ^ (1/2))).

Metode 5 af 5: Sådan normaliseres en vektor i n-dimensionelt rum

• Lad os generalisere formlen til normalisering af en vektor til et rum med et vilkårligt antal dimensioner. For at normalisere vektoren A (a, b, c, ...) er det nødvendigt at finde vektoren u = (a / z, b / z, c / z, ...), hvor z = (a ^ 2 + b ^ 2 + c ^ 2 ...) ^ (1/2).