Indhold

• Trin
• Metode 1 af 3: Sådan løses en kubisk ligning uden et konstant udtryk
• Metode 2 af 3: Sådan finder du hele rødder ved hjælp af multiplikatorer
• Metode 3 af 3: Sådan løses en ligning ved hjælp af diskriminanten

I en kubisk ligning er den højeste eksponent 3, en sådan ligning har 3 rødder (løsninger), og den har formen ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Nogle kubiske ligninger er ikke så lette at løse, men hvis du anvender den rigtige metode (med god teoretisk baggrund), kan du finde rødderne til selv den mest komplekse kubikligning - til dette kan du bruge formlen til at løse den kvadratiske ligning, finde hele rødder, eller bereg den diskriminerende.

Trin

Metode 1 af 3: Sådan løses en kubisk ligning uden et konstant udtryk

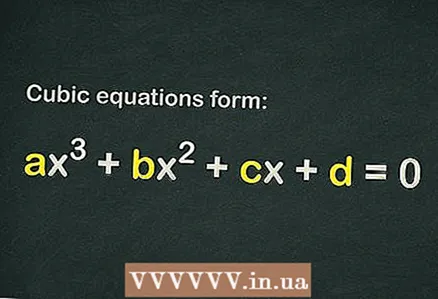1. 1 Find ud af, om der er et frit udtryk i kubikligningen d{ displaystyle d}. Den kubiske ligning har formen ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... For at en ligning kan betragtes som kubisk, er det tilstrækkeligt, at kun udtrykket ${ displaystyle x ^ {3}}$ (det vil sige, at der overhovedet ikke er andre medlemmer).
   • Hvis ligningen har et frit begreb ${ displaystyle d}$, brug en anden metode.
   • Hvis i ligningen ${ displaystyle a = 0}$, det er ikke kubisk.
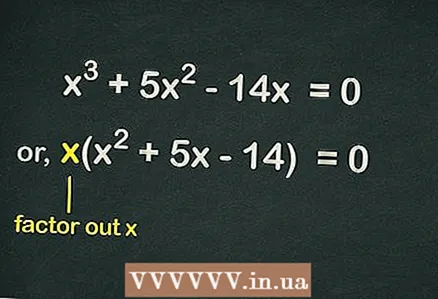2. 2 Tag ud af beslagene x{ displaystyle x}. Da der ikke er noget frit udtryk i ligningen, inkluderer hvert udtryk i ligningen variablen ${ displaystyle x}$... Det betyder, at en ${ displaystyle x}$ kan udelukkes fra parenteser for at forenkle ligningen. Således vil ligningen blive skrevet således: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • For eksempel givet en kubisk ligning ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Tag ud ${ displaystyle x}$ parenteser og få ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
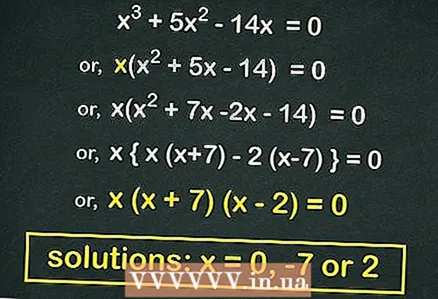3. 3 Faktor (produktet af to binomier) den kvadratiske ligning (hvis muligt). Mange kvadratiske ligninger af formen ${ displaystyle ax ^ {2} + bx + c = 0}$ kan faktoriseres. En sådan ligning vil vise sig, hvis vi tager ud ${ displaystyle x}$ uden for beslagene. I vores eksempel:
   • Tag ud af beslagene ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Faktor den kvadratiske ligning: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Læg hver kasse til ${ displaystyle 0}$... Rødderne til denne ligning er ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Løs en kvadratisk ligning ved hjælp af en speciel formel. Gør dette, hvis den kvadratiske ligning ikke kan faktoriseres. For at finde to rødder af en ligning, værdierne for koefficienterne ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ erstatte i formlen ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • I vores eksempel erstatter værdierne for koefficienterne ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) i formlen:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Første rod:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Anden rod:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Brug nul og kvadratiske rødder som løsninger på den kubiske ligning. Kvadratiske ligninger har to rødder, mens kubiske ligninger har tre. Du har allerede fundet to løsninger - det er rødderne til den kvadratiske ligning. Hvis du sætter "x" uden for parenteserne, ville den tredje løsning være ${ displaystyle 0}$.
   • Hvis du tager "x" ud af parenteserne, får du ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, det vil sige to faktorer: ${ displaystyle x}$ og en kvadratisk ligning i parentes. Hvis nogen af ​​disse faktorer er ${ displaystyle 0}$, hele ligningen er også lig med ${ displaystyle 0}$.
   • Således er to rødder i en kvadratisk ligning løsninger på en kubisk ligning. Den tredje løsning er ${ displaystyle x = 0}$.

Metode 2 af 3: Sådan finder du hele rødder ved hjælp af multiplikatorer

1. 1 Sørg for, at der er et frit udtryk i kubikligningen d{ displaystyle d}. Hvis i en ligning af formen ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ der er et gratis medlem ${ displaystyle d}$ (som ikke er lig med nul), vil det ikke fungere at sætte "x" uden for parenteserne. I dette tilfælde skal du bruge metoden beskrevet i dette afsnit.
   • For eksempel givet en kubisk ligning ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... For at få nul på højre side af ligningen, tilføj ${ displaystyle 6}$ til begge sider af ligningen.
   • Ligningen vil vise sig ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Som ${ displaystyle d = 6}$, kan metoden beskrevet i det første afsnit ikke bruges.
2. 2 Skriv faktorerne for koefficienten ned -en{ displaystyle a} og et gratis medlem d{ displaystyle d}. Det vil sige finde faktorernes tal på ${ displaystyle x ^ {3}}$ og tal før lighedstegnet. Husk, at faktorerne for et tal er de tal, der, når de multipliceres, producerer det tal.
   • For eksempel for at få nummeret 6, du skal multiplicere ${ displaystyle 6 gange 1}$ og ${ displaystyle 2 gange 3}$... Så tallene 1, 2, 3, 6 er faktorer i antallet 6.
   • I vores ligning ${ displaystyle a = 2}$ og ${ displaystyle d = 6}$... Multiplikatorer 2 er 1 og 2... Multiplikatorer 6 er tallene 1, 2, 3 og 6.
3. 3 Opdel hver faktor -en{ displaystyle a} for hver faktor d{ displaystyle d}. Som et resultat får du mange brøker og flere heltal; rødderne i den kubiske ligning vil være et af heltalene eller den negative værdi af et af heltalene.
   • I vores eksempel deler du faktorerne ${ displaystyle a}$ (1 og 2) efter faktorer ${ displaystyle d}$ (1, 2, 3 og 6). Du får: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ og ${ displaystyle { frac {2} {3}}}$... Tilføj nu negative værdier for de opnåede brøker og tal til denne liste: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ og ${ displaystyle - { frac {2} {3}}}$... Hele rødderne i den kubiske ligning er nogle tal fra denne liste.
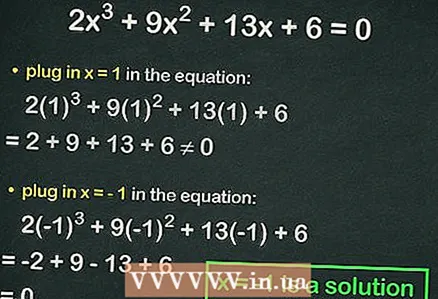4. 4 Sæt hele tal i den kubiske ligning. Hvis ligheden er sand, er det substituerede tal roden til ligningen. For eksempel, erstat i ligningen ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, det vil sige, ligestilling observeres ikke. I dette tilfælde skal du tilslutte det næste nummer.
   • Erstatning ${ displaystyle -1}$: ${ displaystyle (-2) +9 +(- 13) +6}$ = 0. Således, ${ displaystyle -1}$ er hele roden af ​​ligningen.
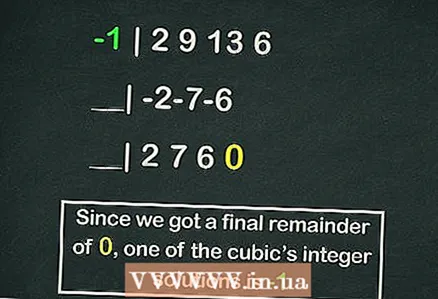5. 5 Brug metoden til at dividere polynomier med Horners ordningat finde rødderne i ligningen hurtigere. Gør dette, hvis du ikke vil manuelt erstatte tal i ligningen. I Horners skema er heltal divideret med værdierne for ligningens koefficienter ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ og ${ displaystyle d}$... Hvis tallene er jævnt delelige (det vil sige, resten er ${ displaystyle 0}$), et heltal er roden til ligningen.
   • Horners skema fortjener en separat artikel, men følgende er et eksempel på beregning af en af ​​rødderne i vores kubiske ligning ved hjælp af denne ordning:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Så resten er ${ displaystyle 0}$, men ${ displaystyle -1}$ er en af ​​ligningens rødder.

Metode 3 af 3: Sådan løses en ligning ved hjælp af diskriminanten

1. 1 Skriv værdierne for ligningens koefficienter ned -en{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} og d{ displaystyle d}. Vi anbefaler, at du på forhånd nedskriver værdierne for de angivne koefficienter for ikke at blive forvirret i fremtiden.
   • For eksempel givet ligningen ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... Skriv ned ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ og ${ displaystyle d = -1}$... Husk at hvis før ${ displaystyle x}$ der er intet tal, den tilsvarende koefficient eksisterer stadig og er lig med ${ displaystyle 1}$.
2. 2 Beregn nul -diskriminanten ved hjælp af en særlig formel. For at løse en kubisk ligning ved hjælp af diskriminanten skal du udføre en række vanskelige beregninger, men hvis du udfører alle trin korrekt, bliver denne metode uundværlig for at løse de mest komplekse kubiske ligninger. Første beregning ${ displaystyle Delta _ {0}}$ (nul diskriminant) er den første værdi, vi har brug for; For at gøre dette skal du erstatte de tilsvarende værdier i formlen ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Diskriminanten er et tal, der kendetegner rødderne til et polynom (for eksempel beregnes diskriminanten af ​​en kvadratisk ligning med formlen ${ displaystyle b ^ {2} -4ac}$).
   • I vores ligning:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Beregn den første diskriminant ved hjælp af formlen Δ1=2b3−9-enbc+27-en2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Første diskriminerende ${ displaystyle Delta _ {1}}$ - dette er den anden vigtige værdi; For at beregne det skal du sætte de tilsvarende værdier i den angivne formel.
   • I vores ligning:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Beregn:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Det vil sige finde diskriminanten af ​​den kubiske ligning gennem de opnåede værdier ${ displaystyle Delta _ {0}}$ og ${ displaystyle Delta _ {1}}$... Hvis diskriminanten af ​​en kubisk ligning er positiv, har ligningen tre rødder; hvis diskriminanten er nul, har ligningen en eller to rødder; hvis diskriminanten er negativ, har ligningen en rod.
   • En kubisk ligning har altid mindst en rod, da grafen for denne ligning skærer X-aksen mindst på et punkt.
   • I vores ligning ${ displaystyle Delta _ {0}}$ og ${ displaystyle Delta _ {1}}$ er lige ${ displaystyle 0}$, så du let kan beregne ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Således har vores ligning en eller to rødder.

5. 5 Beregn:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } højre) div 2}}}$. ${ displaystyle C}$ - dette er den sidste vigtige mængde, der findes; det hjælper dig med at beregne ligningens rødder. Erstat værdierne i den angivne formel ${ displaystyle Delta _ {1}}$ og ${ displaystyle Delta _ {0}}$.
   • I vores ligning:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Find ligningens tre rødder. Gør det med formlen ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, hvor ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, men n er lig med 1, 2 eller 3... Erstat de relevante værdier i denne formel - som et resultat får du tre rødder af ligningen.
   • Beregn værdien ved hjælp af formlen på n = 1, 2 eller 3og tjek derefter svaret. Hvis du får 0, når du tjekker dit svar, er denne værdi roden til ligningen.
   • I vores eksempel, erstat 1 i ${ displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ og få 0, dvs. 1 er en af ​​ligningens rødder.