Indhold

• Trin
• Råd

I modsætning til en lige linje ændres hældningskoefficienten konstant, når den bevæger sig langs kurven. Analyse giver ideen om, at hvert punkt på grafen kan udtrykkes som en vinkelkoefficient eller "øjeblikkelig ændringshastighed". Tangentlinjen ved et punkt er en linje, der har den samme vinkelkoefficient og passerer gennem det samme punkt. For at finde en tangentlinieligning skal du vide, hvordan man udleder den oprindelige ligning.

Trin

Metode 1 af 2: Find ligningen for tangentlinjen

1. 

   Graffunktioner og tangentlinjer (dette trin er valgfrit, men anbefales). Diagrammet hjælper dig lettere med at forstå problemet og kontrollere, om svaret er rimeligt eller ej. Tegn funktionsgrafer på gitterpapir, brug den videnskabelige regnemaskine med graffunktion til reference, hvis det er nødvendigt. Tegn en tangentlinie gennem et givet punkt (Husk at tangentlinjen passerer gennem dette punkt og har samme hældning som grafen der).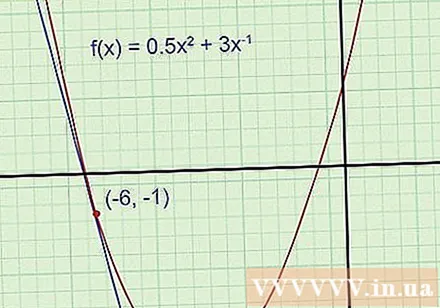
   • Eksempel 1: Parabolsk tegning. Tegn en tangentlinie gennem punktet (-6, -1).
     Selvom du ikke kender tangentligningen, kan du stadig se, at dens hældning er negativ, og ordinaten er negativ (langt under det parabolske toppunkt med ordinaten -5,5). Hvis det endelige svar, der findes, ikke stemmer overens med disse detaljer, skal der være en fejl i din beregning, og du skal kontrollere igen.

2. 

   
   
   Få det første afledte til at finde ligningen hældning af tangentlinjen. Med funktionen f (x) repræsenterer det første afledte f '(x) ligningen for tangentlinjens hældning på et hvilket som helst punkt på f (x). Der er mange måder at tage derivater på. Her er et simpelt eksempel ved hjælp af strømreglen:
   • Eksempel 1 (fortsat): Grafen er givet af en funktion.
     Tilbagekaldelse af magtreglen, når man tager derivater:.
     Det første afledte af funktionen = f '(x) = (2) (0,5) x + 3 - 0.
     f '(x) = x + 3. Erstat x med en hvilken som helst værdi a, ligningen giver os hældningen af ​​tangentlinjefunktionen f (x) i punkt x = a.

3. 

   
   
   Indtast x-værdien for det aktuelle punkt. Læs problemet for at finde koordinaterne til punktet for at finde tangentlinjen. Indtast koordinaten for dette punkt i f '(x). Det opnåede resultat er hældningen af ​​tangentlinjen ved ovenstående punkt.
   • Eksempel 1 (fortsat): Det punkt, der er nævnt i artiklen, er (-6, -1). Brug af diagonal -6 spænding til f '(x):
     f '(- 6) = -6 + 3 = -3
     Tangentlinjens hældning er -3.

4. 

   
   
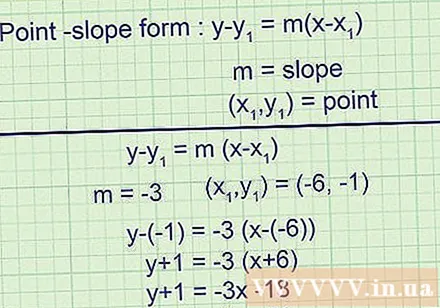
   Skriv en tangentligning i form af en lige linje og kend vinkelkoefficienten og et punkt på den. Denne lineære ligning er skrevet som. Inde, m er hældningen og er et punkt på tangentlinjen. Du har nu alle de oplysninger, du har brug for til at skrive en tangentligning i denne form.
   • Eksempel 1 (fortsat):
     Tangenslinjens hældning er -3, så:
     Tangentlinjen passerer gennem punktet (-6, -1), så den endelige ligning er:
     Kort sagt kan vi:
     

5. 

   Grafisk bekræftelse. Hvis du har en grafregner, skal du tegne den oprindelige funktion og tangentlinjen for at kontrollere, om svaret er korrekt. Hvis du foretager beregninger på papir, skal du bruge grafer tegnet tidligere for at sikre, at der ikke er nogen åbenlyse fejl i dit svar.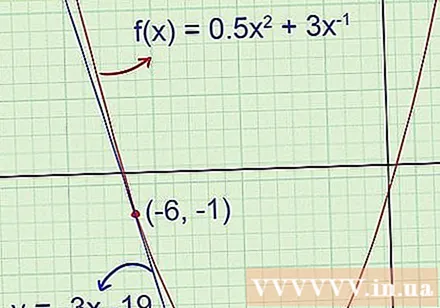
   • Eksempel 1 (fortsat): Den første tegning viser, at tangentlinjen har negative vinkelkoefficienter, og forskydningen er langt under -5,5. Den lige fundet tangensligning er y = -3x -19, hvilket betyder, at -3 er hældningen af ​​vinklen, og -19 er ordinaten.

6. 

   Prøv at løse et vanskeligere problem. Vi gennemgår alle ovenstående trin igen.På dette tidspunkt er målet at finde tangenten til at x = 2: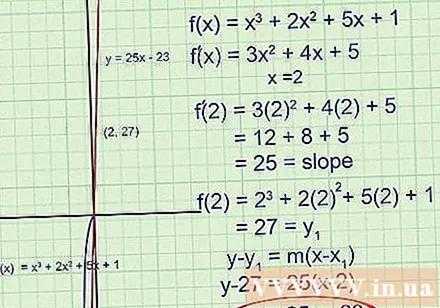
   • Find det første afledte ved hjælp af magtreglen :. Denne funktion giver os tangentens hældning.
   • For x = 2, find. Dette er hældningen ved x = 2.
   • Bemærk, at denne gang har vi ikke et punkt og kun x-koordinaten. For at finde y-koordinaten skal du erstatte x = 2 i den oprindelige funktion :. Resultatet er (2.27).
   • Skriv en ligning for en tangentlinje, der passerer gennem et punkt og har koefficienten for vinklen bestemt:
     
     Reducér om nødvendigt til y = 25x - 23.
   reklame

Metode 2 af 2: Løs relaterede problemer

1. 

   Find det ekstreme på grafen. De er de punkter, hvor grafen nærmer sig et lokalt maksimum (et punkt højere end nabopunkter på begge sider) eller et lokalt minimum (lavere end nabopunkter på begge sider). Tangentlinjen har altid en nulkoefficient på disse punkter (en vandret linje). Imidlertid er vinkelkoefficienten ikke nok til at konkludere, at det er det ekstreme punkt. Sådan finder du dem: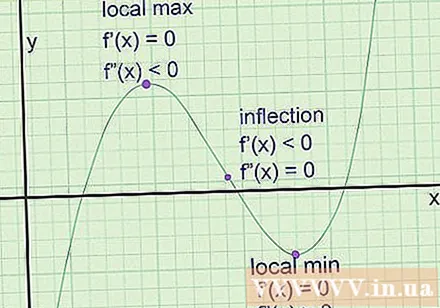
   • Tag det første afledte af funktionen for at få f '(x), hældningen af ​​tangentlinjens hældning.
   • Løs ligningen f '(x) = 0 for at finde det ekstreme punkt potentiel.
   • Ved at tage det kvadratiske derivat for at få f '(x) fortæller ligningen hastigheden på ændring af tangenthældningen.
   • Skift koordinaten ved hver potentiel ekstremitet -en ind i f '' (x). Hvis f '(a) er positiv, har vi et lokalt minimum på -en. Hvis f '(a) er negativ, har vi et lokalt maksimalt punkt. Hvis f '(a) er 0, vil det ikke være det ekstreme, det er et bøjningspunkt.
   • Hvis maks eller min nås kl -en, find f (a) for at bestemme krydset.

2. 

   Find ligningerne for det normale. Den "normale" linje i en kurve ved et givet punkt a passerer gennem dette punkt og er vinkelret på tangentlinjen. For at finde ligningen for det normale skal du bruge følgende: (normal hældning) (normal hældning) = -1, når de passerer det samme punkt på grafen. Specifikt: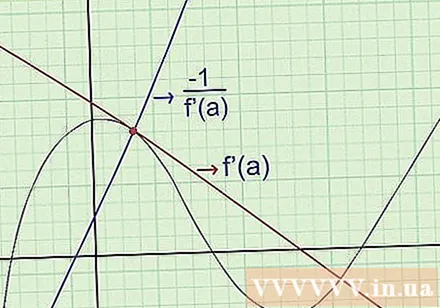
   • Find f '(x), tangentlinjens hældning.
   • Hvis vi på et givet punkt har x = -en: find f '(a) for at bestemme hældningen på det tidspunkt.
   • Beregn for at finde normalens koefficient.
   • Skriv ligningen for vinkelret på at kende koefficienterne for vinklen og et punkt, den passerer igennem.
   reklame

Råd

• Om nødvendigt omskrives den originale ligning i standardform: f (x) = ... eller y = ...