Indhold

• At træde
• Del 1 af 4: Tegning af matrixen
• Del 2 af 4: Læring af operationer til løsning af et system med en matrix
• Del 3 af 4: Flet trinene for at løse galaksen
• Del 4 af 4: Kontrol af din løsning
• Tips

En matrix er en meget nyttig måde at repræsentere tal i et blokformat, som du derefter kan bruge til at løse et system med lineære ligninger. Hvis du kun har to variabler, vil du sandsynligvis bruge en anden metode. Læs om dette i Løsning af et ligningssystem for eksempler på disse andre metoder. Men hvis du har tre eller flere variabler, er en matrix ideel. Ved at bruge gentagne kombinationer af multiplikation og addition kan du systematisk nå frem til en løsning.

At træde

Del 1 af 4: Tegning af matrixen

1. Bekræft, at du har tilstrækkelige data. For at få en unik løsning til hver variabel i et lineært system ved hjælp af en matrix, skal du have så mange ligninger som antallet af variabler, du prøver at løse. For eksempel: med variablerne x, y og z har du brug for tre ligninger. Hvis du har fire variabler, har du brug for fire ligninger.
   • Hvis du har færre ligninger end antallet af variabler, vil du finde ud af nogle grænser for variablerne (såsom x = 3y og y = 2z), men du kan ikke få en præcis løsning. Til denne artikel vil vi kun arbejde hen imod en unik løsning.
2. Skriv dine ligninger i standardformularen. Før du kan placere data fra ligningerne i en matrixform, skal du først skrive hver ligning i standardform. Standardformularen for en lineær ligning er Ax + By + Cz = D, hvor de store bogstaver er koefficienterne (tal), og det sidste tal (D i dette eksempel) er til højre for ligetegnet.
   • Hvis du har flere variabler, skal du bare fortsætte linjen, så længe du har brug for det. For eksempel, hvis du forsøgte at løse et system med seks variabler, ville din standardform ligne Au + Bv + Cw + Dx + Ey + Fz = G. I denne artikel vil vi fokusere på systemer med kun tre variabler. At løse en større galakse er nøjagtig den samme, men det tager bare mere tid og flere trin.
   • Bemærk, at i standardform er operationerne mellem vilkårene altid en tilføjelse. Hvis der er en subtraktion i din ligning, i stedet for en tilføjelse, bliver du nødt til at arbejde med dette senere ved at gøre din koefficient negativ. For at gøre det lettere at huske kan du omskrive ligningen og tilføje operationen og gøre koefficienten negativ. For eksempel kan du omskrive ligningen 3x-2y + 4z = 1 som 3x + (- 2y) + 4z = 1.
3. Placer tallene fra ligningssystemet i en matrix. En matrix er en gruppe af tal, arrangeret i en slags tabel, som vi vil arbejde med at løse systemet med. Det indeholder grundlæggende de samme data som ligningerne selv, men i et enklere format. For at lave matricen for dine ligninger i standardform skal du bare kopiere koefficienterne og resultatet af hver ligning i en enkelt række og stable disse rækker oven på hinanden.
   • Antag at du har et system bestående af de tre ligninger 3x + y-z = 9, 2x-2y + z = -3 og x + y + z = 7. Den øverste række i din matrix indeholder tallene 3, 1, -1, 9, da disse er koefficienterne og løsningen af ​​den første ligning. Bemærk, at enhver variabel, der ikke har en koefficient, antages at have en koefficient på 1. Den anden række i matrixen bliver 2, -2, 1, -3, og den tredje række bliver 1, 1, 1, 7.
   • Sørg for at justere x-koefficienterne i den første kolonne, y-koefficienterne i den anden, z-koefficienterne i den tredje og løsningsbetingelserne i den fjerde. Når du er færdig med at arbejde med matrixen, vil disse kolonner være vigtige, når du skriver din løsning.
4. Tegn en stor firkantet parentes omkring hele din matrix. Efter konvention er en matrix angivet med et par firkantede parenteser [] omkring hele talblokken. Beslagene påvirker ikke løsningen på nogen måde, men de indikerer, at du arbejder med matricer. En matrix kan bestå af et vilkårligt antal rækker og kolonner. I denne artikel bruger vi parenteser omkring udtryk i træk for at indikere, at de hører sammen.
5. Brug af fælles symbolik. Når du arbejder med matricer, er det almindeligt at henvise til rækkerne med forkortelsen R og kolonnerne med forkortelsen C. Du kan bruge tal sammen med disse bogstaver til at angive en bestemt række eller kolonne. For eksempel for at angive række 1 i en matrix kan du skrive R1. Række 2 bliver derefter R2.
   • Du kan angive en hvilken som helst specifik position i en matrix ved hjælp af en kombination af R og C. For eksempel for at angive et udtryk i anden række, tredje kolonne, kan du kalde det R2C3.

Del 2 af 4: Læring af operationer til løsning af et system med en matrix

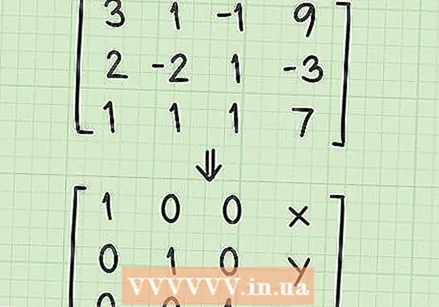1. Forstå formen på løsningsmatrixen. Inden du begynder at løse dit ligningssystem, skal du forstå, hvad du skal gøre med matrixen. På dette tidspunkt har du en matrix, der ser sådan ud:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • Du arbejder med en række grundlæggende operationer for at oprette "løsningsmatrix". Løsningsmatrixen vil se sådan ud:
   • 1 0 0 x
   • 0 1 0 år
   • 0 0 1 z
   • Bemærk, at matrixen består af 1'er i en diagonal linje med 0'er i alle andre mellemrum undtagen den fjerde kolonne. Tallene i den fjerde kolonne er løsningen på variablerne x, y og z.
2. Brug skalar multiplikation. Det første værktøj, du har til rådighed til at løse et system ved hjælp af en matrix, er skalær multiplikation. Dette er simpelthen et udtryk, der betyder, at du multiplicerer elementerne i en række af matrixen med et konstant tal (ikke en variabel). Når du bruger skalar multiplikation, skal du huske på, at du skal gange hver periode i hele rækken med det nummer, du vælger. Hvis du glemmer den første periode og bare ganger dig, får du den forkerte løsning. Du behøver dog ikke multiplicere hele matrixen på samme tid. I skalar multiplikation arbejder du kun på en række ad gangen.
   • Det er almindeligt at bruge fraktioner i skalar multiplikation, fordi du ofte vil have en diagonal række på 1'er. Bliv vant til at arbejde med fraktioner. Det vil også være lettere (for de fleste trin i løsning af matrixen) at være i stand til at skrive dine brøker i forkert form og derefter konvertere dem tilbage til blandede tal for den endelige løsning. Derfor er tallet 1 2/3 lettere at arbejde med, hvis du skriver det som 5/3.
   • For eksempel starter den første række (R1) i vores eksempelproblem med udtrykkene [3,1, -1,9]. Opløsningsmatrixen skal indeholde en 1 i første position i første række. For at "ændre" 3 til en 1 kan vi gange hele rækken med 1/3. Dette skaber den nye R1 på [1,1 / 3, -1 / 3,3].
   • Sørg for at efterlade eventuelle negative tegn, hvor de hører hjemme.
3. Brug række tilføjelse eller række subtraktion. Det andet værktøj, du kan bruge, er at tilføje eller trække to rækker i matrixen. For at oprette 0-termerne i din løsningsmatrix skal du tilføje eller trække tal for at komme til 0. For eksempel, hvis R1 er af en matrix [1,4,3,2] og R2 er [1,3,5,8], så kan du trække den første række fra den anden række og oprette en ny række [0, -1, 2.6], fordi 1-1 = 0 (første kolonne), 3-4 = -1 (anden kolonne), 5-3 = 2 (tredje kolonne) og 8-2 = 6 (fjerde kolonne). Når du udfører en rækkeaddition eller radtrækning, skal du omskrive dit nye resultat i stedet for den række, du startede med. I dette tilfælde udtrækker vi række 2 og indsætter den nye række [0, -1,2,6].
   • Du kan bruge en stenografisk notation og erklære denne handling som R2-R1 = [0, -1,2,6].
   • Husk at addition og subtraktion er lige modsatte former for den samme operation. Tænk på det som at tilføje to tal eller trække det modsatte. For eksempel, hvis du starter med den enkle ligning 3-3 = 0, kan du tænke på dette som et tilføjelsesproblem på 3 + (- 3) = 0. Resultatet er det samme. Dette virker simpelt, men det er undertiden lettere at overveje et problem i en eller anden form. Bare hold øje med dine negative tegn.
4. Kombiner rækkeaddition og skalar multiplikation i et enkelt trin. Du kan ikke forvente, at vilkårene altid matcher, så du kan bruge en simpel tilføjelse eller subtraktion til at oprette 0'er i din matrix. Oftere bliver du nødt til at tilføje (eller trække) et multiplum fra en anden række. For at gøre dette skal du først udføre den skalære multiplikation og derefter føje resultatet til den målrække, du prøver at ændre.
   • Formode; at der er en række 1 på [1,1,2,6] og en række 2 på [2,3,1,1]. Du vil have et 0-udtryk i den første kolonne i R2. Det vil sige, at du vil ændre 2 til en 0. For at gøre dette skal du trække en 2. Du kan få en 2 ved først at gange række 1 med den skalære multiplikation 2 og derefter trække den første række fra den anden række. I kort form kan dette skrives ned som R2-2 * R1. Først skal du gange R1 med 2 for at få [2,2,4,12]. Træk derefter dette fra R2 for at få [(2-2), (3-2), (1-4), (1-12)]. Forenkle dette, og din nye R2 bliver [0,1, -3, -11].
5. Kopier rækker, der forbliver uændrede, mens du arbejder. Når du arbejder på matrixen, vil du ændre en enkelt række ad gangen, enten ved skalamultiplikation, rækkeaddition eller rækkeunderskud eller en kombination af trin. Når du ændrer en række, skal du sørge for at kopiere de andre rækker i din matrix i deres oprindelige form.
   • En almindelig fejl opstår, når der udføres et kombineret multiplikations- og tilføjelsestrin i et træk. Sig for eksempel, at du skal trække R1 fra R2 to gange. Når du gange R1 med 2 for at udføre dette trin, skal du huske at R1 ikke ændres i matrixen. Du udfører kun multiplikationen for at ændre R2. Kopier først R1 i sin oprindelige form, og foretag derefter ændringen til R2.
6. Første arbejde fra top til bund. For at løse systemet arbejder du i et meget organiseret mønster og i det væsentlige "løser" et udtryk af matrixen ad gangen. Sekvensen for et tre-variabelt array vil se sådan ud:
   • 1. Lav en 1 i første række, første kolonne (R1C1).
   • 2. Lav et 0 i anden række, første kolonne (R2C1).
   • 3. Lav en 1 i anden række, anden kolonne (R2C2).
   • 4. Lav et 0 i tredje række, første kolonne (R3C1).
   • 5. Lav et 0 i tredje række, anden kolonne (R3C2).
   • 6. Lav en 1 i tredje række, tredje kolonne (R3C3).
7. Arbejd tilbage fra bunden til toppen. På dette tidspunkt er du halvvejs gennem løsningen, hvis du udførte trinene korrekt. Du skal have den diagonale linje på 1, med 0 under den. Tallene i den fjerde kolonne betyder ikke noget på dette tidspunkt. Nu arbejder du tilbage til toppen som følger:
   • Opret et 0 i anden række, tredje kolonne (R2C3).
   • Opret et 0 i første række, tredje kolonne (R1C3).
   • Opret et 0 i første række, anden kolonne (R1C2).
8. Kontroller, om du har oprettet løsningsmatrixen. Hvis dit arbejde er korrekt, har du oprettet løsningsmatrixen med 1'er i en diagonal linje på R1C1, R2C2, R3C3 og 0'er i de andre positioner i de første tre kolonner. Tallene i den fjerde kolonne er løsningerne til dit lineære system.

Del 3 af 4: Flet trinene for at løse galaksen

1. Start med et eksempel på et system med lineære ligninger. For at øve disse trin, lad os starte med det system, vi brugte tidligere: 3x + y-z = 9, 2x-2y + z = -3 og x + y + z = 7. Hvis du skriver dette i en matrix, har du R1 = [3,1, -1,9], R2 = [2, -2,1, -3] og R3 = [1,1,1,7].
2. Opret en 1 i første position R1C1. Bemærk, at R1 starter med en 3 på dette tidspunkt. Du skal ændre den til en 1. Du kan gøre dette ved skalar multiplikation, gang alle fire termer af R1 med 1/3. Kort sagt kan du skrive som R1 * 1/3. Dette giver et nyt resultat for R1, hvis R1 = [1,1 / 3, -1 / 3,3]. Kopi R2 og R2, uændret, når R2 = [2, -2,1, -3] og R3 = [1,1,1,7].
   • Bemærk, at multiplikation og division kun er omvendte funktioner i hinanden. Vi kan sige, at vi gange med 1/3 eller dividerer med 3 uden at ændre resultatet.
3. Opret et 0 i anden række, første kolonne (R2C1). På dette tidspunkt er R2 = [2, -2,1, -3]. For at komme tættere på løsningsmatrixen skal du ændre den første periode fra en 2 til en 0. Du kan gøre dette ved at trække dobbelt så meget som R1, da R1 starter med en 1. Kort sagt er operationen R2- 2 * R1. Husk, du ændrer ikke R1, bare arbejd med det. Så første kopi R1, hvis R1 = [1,1 / 3, -1 / 3,3]. Så hvis du fordobler hver periode på R1, får du 2 * R1 = [2,2 / 3, -2 / 3,6]. Til sidst trækker du dette resultat fra den oprindelige R2 for at få din nye R2. Arbejdsperiode for udtryk bliver denne subtraktion (2-2), (-2-2 / 3), (1 - (- 2/3)), (-3-6). Vi forenkler disse til den nye R2 = [0, -8 / 3,5 / 3, -9]. Bemærk, at den første periode er 0 (uanset hvad dit mål var).
   • Skriv række 3 (som ikke er ændret) som R3 = [1,1,1,7].
   • Vær forsigtig, når du trækker negative tal for at sikre, at tegnene forbliver korrekte.
   • Lad os først lade fraktionerne være i deres forkerte form. Dette letter senere trin i løsningen. Du kan forenkle brøkene i det sidste trin i problemet.
4. Opret en 1 i anden række, anden kolonne (R2C2). For at fortsætte med at danne den diagonale linje på 1'er skal du konvertere den anden sigt -8/3 til 1. Gør dette ved at gange hele rækken med det gensidige af dette nummer (-3/8). Symbolisk er dette trin R2 * (- 3/8). Den resulterende anden række er R2 = [0,1, -5 / 8,27 / 8].
   • Bemærk, at hvis den venstre halvdel af rækken begynder at ligne løsningen med 0 og 1, kan den højre halvdel begynde at se grim ud med ukorrekte fraktioner. Lad dem bare være, hvad de er for nu.
   • Glem ikke at fortsætte med at kopiere de uberørte rækker, så R1 = [1,1 / 3, -1 / 3,3] og R3 = [1,1,1,7].
5. Opret et 0 i tredje række, første kolonne (R3C1). Dit fokus flyttes nu til tredje række, R3 = [1,1,1,7]. For at lave et 0 i den første position skal du trække en 1 fra den 1, der i øjeblikket er i den position. Hvis du kigger op, er der en 1 på første position på R1. Så du skal bare trække R1 fra R3 for at få det ønskede resultat. Arbejdsperiode for periode, dette bliver (1-1), (1-1 / 3), (1 - (- 1/3)), (7-3). Disse fire mini-problemer kan derefter forenkles til den nye R3 = [0.2 / 3.4 / 3.4].
   • Fortsæt med at kopiere langs R1 = [1.1 / 3, -1 / 3.3] og R2 = [0.1, -5 / 8.27 / 8]. Husk, at du kun skifter en række ad gangen.
6. Lav et 0 i tredje række, anden kolonne (R3C2). Denne værdi er i øjeblikket 2/3, men skal konverteres til en 0. Ved første øjekast ser det ud til, at du kan trække R1-værdierne med dobbelt, da den tilsvarende kolonne med R1 indeholder en 1/3. Men hvis du fordobler og trækker alle værdierne for R1, ændres 0 i den første kolonne af R3, hvilket du ikke vil have. Dette ville være et skridt tilbage i din løsning. Så du er nødt til at arbejde med en kombination af R2. Ved at trække 2/3 fra R2 oprettes et 0 i den anden kolonne uden at ændre den første kolonne. I kort form er dette R3-2 / 3 * R2. De enkelte vilkår bliver (0-0), (2 / 3-2 / 3), (4/3 - (- 5/3 * 2/3)), (4-27 / 8 * 2/3) . Forenkling giver derefter R3 = [0,0,42 / 24,42 / 24].
7. Opret en 1 i tredje række, tredje kolonne (R3C3). Dette er en simpel multiplikation med det gensidige af det tal, det står. Den aktuelle værdi er 42/24, så du kan gange med 24/42 for at få den ønskede værdi 1. Bemærk, at de to første termer begge er 0, så enhver multiplikation forbliver 0. Den nye værdi af R3 = [0,0,1,1].
   • Bemærk, at de fraktioner, der syntes ret komplicerede i det foregående trin, allerede begynder at løse.
   • Fortsæt med R1 = [1.1 / 3, -1 / 3.3] og R2 = [0.1, -5 / 8.27 / 8].
   • Bemærk, at du på dette tidspunkt har diagonalen 1 til din løsningsmatrix. Du skal kun konvertere tre elementer i matrixen til 0'er for at finde din løsning.
8. Opret et 0 i anden række, tredje kolonne. R2 er i øjeblikket [0,1, -5 / 8,27 / 8] med en værdi på -5/8 i den tredje kolonne. Du skal omdanne den til en 0. Det betyder, at du skal udføre en eller anden operation med R3, der består i at tilføje 5/8. Da den tilsvarende tredje kolonne i R3 er en 1, skal du gange alle værdierne for R3 med 5/8 og tilføje resultatet til R2. Kort sagt er dette R2 + 5/8 * R3. Udtryk for udtryk er R2 = (0 + 0), (1 + 0), (-5 / 8 + 5/8), (27/8 + 5/8). Dette kan forenkles til R2 = [0,1,0,4].
   • Kopier derefter R1 = [1,1 / 3, -1 / 3,3] og R3 = [0,0,1,1].
9. Opret et 0 i første række, tredje kolonne (R1C3). Den første række er i øjeblikket R1 = [1,1 / 3, -1 / 3,3]. Du skal konvertere -1/3 i den tredje kolonne til en 0 ved hjælp af en kombination af R3. Du vil ikke bruge R2, fordi 1 i den anden kolonne i R2 vil ændre R1 på den forkerte måde. Så du multiplicerer R3 * 1/3 og tilføjer resultatet til R1. Notationen for dette er R1 + 1/3 * R3. Udtrykket for termudarbejdelse resulterer i R1 = (1 + 0), (1/3 + 0), (-1 / 3 + 1/3), (3 + 1/3). Du kan forenkle dette til en ny R1 = [1,1 / 3,0,10 / 3].
   • Kopier den uændrede R2 = [0,1,0,4] og R3 = [0,0,1,1].
10. Lav et 0 i første række, anden kolonne (R1C2). Hvis alt er gjort korrekt, skal dette være det sidste trin. Du skal konvertere 1/3 i anden kolonne til en 0. Du kan få dette ved at gange og trække R2 * 1/3. Kort fortalt er dette R1-1 / 3 * R2. Resultatet er R1 = (1-0), (1 / 3-1 / 3), (0-0), (10 / 3-4 / 3). Forenkling giver derefter R1 = [1,0,0,2].
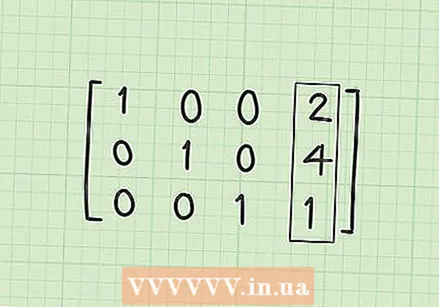11. Søg efter løsningsmatrixen. På dette tidspunkt, hvis alt gik godt, ville du have de tre rækker R1 = [1,0,0,2], R2 = [0,1,0,4] og R3 = [0,0,1,1] skal have. Bemærk, at hvis du skriver dette i blokmatrixform med rækkerne oven over hinanden, har du diagonale 1'er med 0'er længere, og dine løsninger er i den fjerde kolonne. Løsningsmatrixen skal se sådan ud:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. Forståelse af din løsning. Efter konvertering af de lineære ligninger til en matrix placerer du x-koefficienterne i den første kolonne, y-koefficienterne i den anden kolonne, z-koefficienterne i den tredje kolonne. Hvis du vil omskrive matrixen til ligninger igen, betyder disse tre linjer i matrixen faktisk de tre ligninger 1x + 0y + 0z = 2, 0x + 1y + 0z = 4 og 0x + 0y + 1z = 1. Da vi kan krydse 0-termerne og ikke behøver at skrive 1-koefficienterne, forenkler disse tre ligninger løsningen, x = 2, y = 4 og z = 1. Dette er løsningen på dit system med lineære ligninger.

Del 4 af 4: Kontrol af din løsning

1. Inkluder løsningerne i hver variabel i hver ligning. Det er altid en god ide at kontrollere, om din løsning faktisk er korrekt. Du gør dette ved at teste dine resultater i de originale ligninger.
   • De oprindelige ligninger for dette problem var: 3x + y-z = 9, 2x-2y + z = -3 og x + y + z = 7. Når du erstatter variablerne med deres værdier, du fandt, får du 3 * 2 + 4-1 = 9, 2 * 2-2 * 4 + 1 = -3 og 2 + 4 + 1 = 7.
2. Forenkle enhver sammenligning. Udfør operationerne i hver ligning i henhold til de grundlæggende regler for operationerne. Den første ligning forenkles til 6 + 4-1 = 9 eller 9 = 9. Den anden ligning kan forenkles til 4-8 + 1 = -3 eller -3 = -3. Den sidste ligning er simpelthen 7 = 7.
   • Da enhver ligning forenkles til en ægte matematikerklæring, er dine løsninger korrekte. Hvis nogen af ​​løsningerne er forkerte, skal du kontrollere dit arbejde igen og se efter eventuelle fejl. Nogle almindelige fejl opstår, når man slipper af minustegn undervejs eller forveksler multiplikation og tilføjelse af brøker.
3. Skriv dine endelige løsninger. For dette givne problem er den endelige løsning x = 2, y = 4 og z = 1.

Tips

• Hvis dit ligningssystem er meget komplekst med mange variabler, kan du muligvis bruge en grafregner i stedet for at udføre arbejdet manuelt. For information om dette kan du også konsultere wikiHow.