Indhold

• Trin
• Tips

Den rationelle funktion har formen y = N (x) / D (x), hvor N og D er polynomer. For at plotte en sådan funktion præcist har du brug for et godt kendskab til algebra, herunder differentialberegninger. Overvej følgende eksempel: y = (2x - 6x + 5)/(4x + 2).

Trin

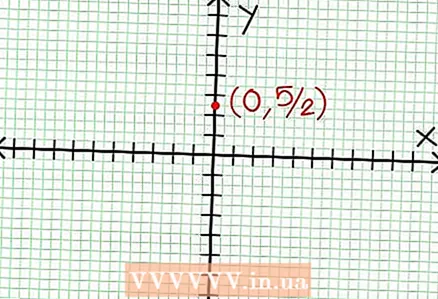1. 1 Find y-afsnit af grafen. For at gøre dette skal du erstatte x = 0 i funktionen og få y = 5/2. Således har skæringspunktet for grafen med Y -aksen koordinater (0, 5/2).Placer dette punkt på koordinatplanet.
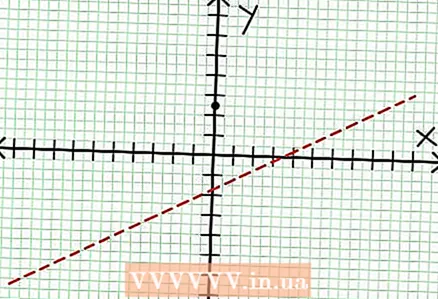2. 2 Find de vandrette asymptoter. Opdel tælleren med nævneren (i en kolonne) for at bestemme "y "'s adfærd med værdier af" x ", der har tendens til uendelig. I vores eksempel vil opdelingen være y = (1/2)x - (7/4) + 17/(8x + 4). For store positive eller negative værdier på "x" 17 / (8x + 4) har en tendens til nul, og grafen nærmer sig den lige linje givet af funktionen y = (1/2)x - (7/4). Plot denne funktion ved hjælp af den stiplede linje.
   • Hvis tællerens grad er mindre end nævneren, kan du ikke dividere tælleren med nævneren, og asymptoten vil blive beskrevet af funktionen på = 0.
   • Hvis tællergraden er lig med nævnergraden, er asymptoten en vandret linje, der er lig med forholdet mellem koefficienterne ved "x" i den højeste grad.
   • Hvis tællerens grad er 1 mere end nævnergraden, er asymptoten en skrå lige linje, hvis hældning er lig med forholdet mellem koefficienterne ved "x" til den højeste grad.
   • Hvis tællerens grad er større end nævneren med 2, 3 osv., Så for store værdier |NS| betyder på tendens til uendelighed (positiv eller negativ) i form af en firkant, kubik eller anden grad af et polynom. I dette tilfælde behøver du sandsynligvis ikke at opbygge en nøjagtig graf over den funktion, der opnås ved at dividere tælleren med nævneren.
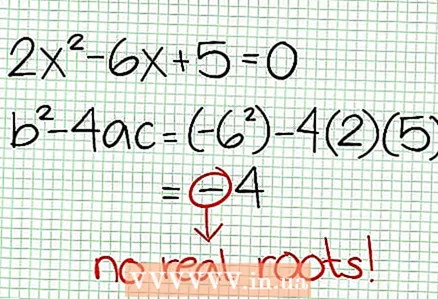3. 3 Find funktionens nuller. En rationel funktion har nuller, når tælleren er nul, det vil sige N (NS) = 0. I vores eksempel 2x - 6x + 5 = 0. Diskriminanten af ​​denne kvadratiske ligning: b - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Da diskriminanten er negativ, så er N (NS), og dermed F (NS) har ingen rigtige rødder. Grafen for en rationel funktion skærer ikke X-aksen. Hvis funktionen har nuller (rødder), skal du sætte dem på koordinatplanet.
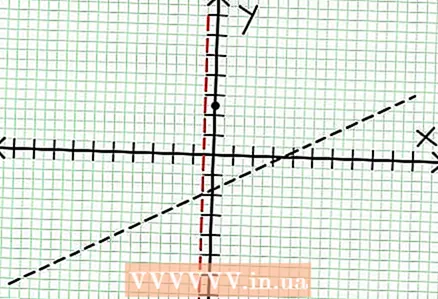4. 4 Find de lodrette asymptoter. For at gøre dette skal du sætte nævneren til nul. I vores eksempel 4x + 2 = 0 og NS = -1/2. Plot den lodrette asymptote ved hjælp af den stiplede linje. Hvis for en vis værdi NS N (NS) = 0 og D (NS) = 0, så eksisterer den lodrette asymptote enten eller findes ikke (dette er et sjældent tilfælde, men det er bedre at huske det).
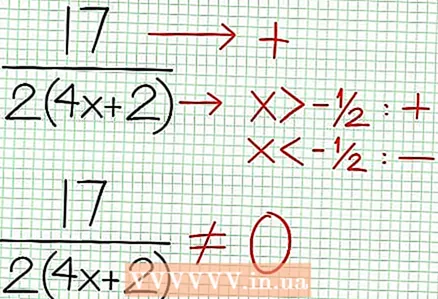5. 5 Se på resten af ​​tælleren divideret med nævneren. Er det positivt, negativt eller nul? I vores eksempel er resten 17, hvilket er positivt. Nævner 4x + 2 positive til højre for den lodrette asymptote og negative til venstre for den. Det betyder, at grafen over den rationelle funktion for store positive værdier NS nærmer sig asymptoten ovenfra, og for store negative værdier NS - nedefra. Siden 17 / (8x + 4) er aldrig lig med nul, så skærer grafen for denne funktion aldrig den lige linje, der er angivet af funktionen på = (1/2)NS - (7/4).
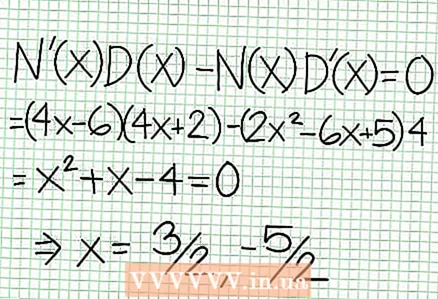6. 6 Find lokal ekstrema. Der findes et lokalt ekstremum for N '(x) D (x) - N (x) D ’(x) = 0. I vores eksempel er N ’(x) = 4x - 6 og D '(x) = 4. N ’(x) D (x) - N (x) D ’(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Ved at løse denne ligning finder du det x = 3/2 og x = -5/2. (Disse er ikke helt nøjagtige værdier, men de er velegnede til vores tilfælde, når der ikke er brug for superpræcision.)
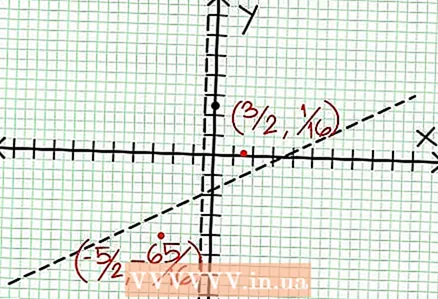7. 7 Find værdien på for hver lokal ekstremum. For at gøre dette skal du erstatte værdierne NS ind i den oprindelige rationelle funktion. I vores eksempel er f (3/2) = 1/16 og f (-5/2) = -65/16. Afsæt punkter (3/2, 1/16) og (-5/2, -65/16) på koordinatplanet. Da beregningerne er baseret på omtrentlige værdier (fra det foregående trin), er minimum og maksimum fundet heller ikke helt nøjagtige (men sandsynligvis meget tæt på de nøjagtige værdier). (Punktet (3/2, 1/16) er meget tæt på det lokale minimum. Fra trin 3 ved vi det på altid positiv til NS> -1/2, og vi fandt en lille værdi (1/16); fejlværdien er derfor ekstremt lille i dette tilfælde.)
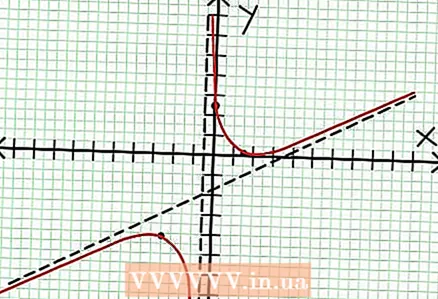8. 8 Forbind de afventende punkter og udfør jævnt grafen til asymptoterne (glem ikke den korrekte retning for grafen, der nærmer sig asymptoterne). Husk, at grafen ikke må krydse X-aksen (se trin 3). Grafen skærer heller ikke med de vandrette og lodrette asymptoter (se trin 5). Ændre ikke diagrammets retning undtagen på de ekstreme punkter, der blev fundet i det foregående trin.

Tips

• Hvis du fulgte ovenstående trin strengt i rækkefølge, er det ikke nødvendigt at beregne de anden derivater (eller lignende komplekse mængder) for at teste din løsning.
• Hvis du ikke behøver at beregne værdierne for mængder, kan du erstatte at finde lokalt ekstrema ved at beregne nogle yderligere par koordinater (NS, på) mellem hvert par asymptoter. Desuden, hvis du er ligeglad med, hvordan den beskrevne metode fungerer, skal du ikke blive overrasket over, hvorfor du ikke kan finde derivatet og løse ligningen N '(x) D (x) - N (x) D ’(x) = 0.
• I nogle tilfælde bliver du nødt til at arbejde med polynom af højere orden. Hvis du ikke kan finde den nøjagtige løsning ved hjælp af faktorisering, formler osv., Skal du estimere mulige løsninger ved hjælp af numeriske metoder som Newtons metode.
• I sjældne tilfælde deler tæller og nævner en fælles variabelfaktor. Ifølge de beskrevne trin vil dette føre til nul og en lodret asymptote samme sted. Dette er imidlertid ikke muligt, og forklaringen er en af ​​følgende:
  • Nul i N (NS) har en større multiplicitet end nul i D (NS). Graf F (NS) har en tendens til nul på dette tidspunkt, men er ikke defineret der. Angiv dette ved at tegne en cirkel omkring punktet.
  • Nul i N (NS) og nul i D (NS) har den samme mangfoldighed. Grafen nærmer sig et ikke-nulpunkt ved denne værdi NSmen ikke defineret deri. Angiv dette ved at tegne en cirkel omkring punktet.
  • Nul i N (NS) har en lavere multiplicitet end nul i D (NS). Der er en lodret asymptote her.